））如图（a）所示，一导热性能良好、内壁光滑的气缸水平放置，横截面积为S＝2×10 3m2、质量为m＝4kg厚度不计的活塞与气缸底部之间封闭了一部分气体，此时活塞与气缸底部之间的距离为24cm，在活塞的右侧12cm处有一对与气缸固定连接的卡环，气体的温度为300K，大气压强P0＝1.0×105Pa。现将气缸竖直放置，如图（b）所示，取g＝10m/s2。求：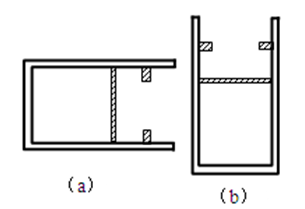
①活塞与气缸底部之间的距离；
②加热到675K时封闭气体的压强。
用油膜法可粗略测出阿伏加德罗常数，把密度ρ=0.8×103 kg/m3的某种油，用滴管滴出一滴油在水面上形成油膜，已知这滴油的体积V=0.5×10-3 cm3，形成的油膜的面积S="0.7" m2，油的摩尔质量Ml="0.09" kg/mol.若把油膜看成单分子层，每个油分子看成球形，那么：
(a)油分子的直径为多大？
(b)由以上数据可测出的阿伏加德罗常数大约为多少？（保留一位有效数字）
如图甲所示，两平行金属板A、B的板长L=0．2m，板间距d=0．2m，两金属板间加如图乙所示的交变电压，并在两板间形成交变的匀强电场，忽略其边缘效应，在金属板上侧有一方向垂直于纸面向里的匀强磁场，其上下宽度D= 0．4m，左右范围足够大，边界MN和PQ均与金属板垂直，匀强磁场的磁感应强度B =1×l0－2T．在极板下侧中点O处有一粒子源，从t=0时起不断地沿着OO’发射比荷
=1×l08 C/kg．初速度为v0=2×l05m/s的带正电粒子，忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极板间的电压变化．
（1）求粒子进入磁场时的最大速率；
（2）对于能从MN边界飞出磁场的粒子，其在磁场的入射点和出射点的间距s是否为定值？若是，求该值；若不是，求s与粒子由O出发的时刻t之间的关系式；
（3）定义在磁场中飞行时间最长的粒子为{A类粒子}，求出{A类粒子}在磁场中飞行的时间，以及由O出发的可能时刻．
如图所示，质量为M的光滑长木板静止在光滑水平地面上，左端固定一劲度系数为k的水平轻质弹簧，右侧用一不可伸长的细绳连接于竖直墙上，细绳所能承受的最大拉力为FT，使一质量为m、初速度为v0的小物体，在木板上无摩擦地向左滑动而后压缩弹簧，细绳被拉断，不计细绳被拉断时的能量损失．弹簧的弹性势能表达式为Ep=
kx2（k为弹簧的劲度系数，x为弹簧的形变量）．
（1）要使细绳被拉断，vo应满足怎样的条件？
（2）若小物体最后离开长木板时相对地面速度恰好为零，请在坐标系中定性画出从小物体接触弹簧到与弹簧分离的过程小物体的v—t图像；
（3）若长木板在细绳拉断后被加速的过程中，所能获得的最大加速度为aM，求此时小物体的速度．
如图甲，电阻为R=2
的金属线圈与一平行粗糙轨道相连并固定在水平面内，轨道间 距为d =0.5m，虚线右侧存在垂直于纸面向里的匀强磁场，磁感应强度为B1=0．1T，磁场内外分别静置垂直于导轨的金属棒P和Q，其质量m1=m2= 0．02kg，电阻R1=R2= 2．t=0时起对左侧圆形线圈区域施加一个垂直于纸面的交变磁场B2，使得线圈中产生如图乙所示的正弦交变电流（从M端流出时为电流正方向），整个过程两根金属棒都没有滑动，不考虑P和Q电流的磁场以及导轨电阻．取重力加速度g= l0m/s2，
（1）若第1s内线圈区域的磁场B2正在减弱，则其方向应是垂直纸面向里还是向外？
（2）假设最大静摩擦力等于滑动摩擦力，金属棒与导轨间的滑动摩擦因数至少应是多少？
（3）求前4s内回路产生的总焦耳热．
的速率反弹，试通过计算判断发生的是不是弹性碰撞．
粤公网安备 44130202000953号