5分)八(2)班组织了一次环保知识竞赛,甲乙两队各5人的成绩如下表所示(10分制).
| 甲 |
9 |
8 |
10 |
6 |
9 |
| 乙 |
8 |
7 |
8 |
9 |
10 |
(1)指出甲队成绩的中位数;
(2)指出乙队成绩的众数;
(3)若计算出方差为: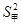 =1.84,
=1.84,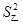 =1.04,判断哪队的成绩更整齐?
=1.04,判断哪队的成绩更整齐?
相关知识点
推荐套卷
5分)八(2)班组织了一次环保知识竞赛,甲乙两队各5人的成绩如下表所示(10分制).
| 甲 |
9 |
8 |
10 |
6 |
9 |
| 乙 |
8 |
7 |
8 |
9 |
10 |
(1)指出甲队成绩的中位数;
(2)指出乙队成绩的众数;
(3)若计算出方差为: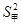 =1.84,
=1.84,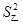 =1.04,判断哪队的成绩更整齐?
=1.04,判断哪队的成绩更整齐?