如图1,在四边形ABCD中,∠ABC+∠ADC=180°,BE、DF分别是∠ABC与∠ADC的平分线,∠ADF与∠AFD互余.
(1)试判断直线BE与DF的位置关系,并说明理由;
(2)如图2,延长CB、DF相交于点G,过点B作BH⊥FG,垂足为点H,试判断∠FBH与∠GBH的大小关系,并说明理由.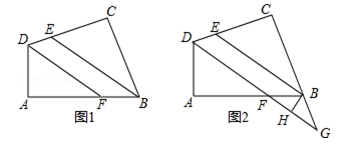
如图1,在四边形ABCD中,∠ABC+∠ADC=180°,BE、DF分别是∠ABC与∠ADC的平分线,∠ADF与∠AFD互余.
(1)试判断直线BE与DF的位置关系,并说明理由;
(2)如图2,延长CB、DF相交于点G,过点B作BH⊥FG,垂足为点H,试判断∠FBH与∠GBH的大小关系,并说明理由.