如图所示,ABCD是封装手机LED闪光灯的圆柱形玻璃体的轴截面,玻璃体的厚度为d。厚度不计半径为r的圆形LED灯贴在玻璃体CD面上,圆心与CD面中心P重合,其发出的光从AB面射出,玻璃的折射率为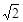 。不考虑光在AD和BC面上的反射,AB面上都有光线射出,求玻璃体的最大半径。
。不考虑光在AD和BC面上的反射,AB面上都有光线射出,求玻璃体的最大半径。
如图所示,ABCD是封装手机LED闪光灯的圆柱形玻璃体的轴截面,玻璃体的厚度为d。厚度不计半径为r的圆形LED灯贴在玻璃体CD面上,圆心与CD面中心P重合,其发出的光从AB面射出,玻璃的折射率为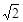 。不考虑光在AD和BC面上的反射,AB面上都有光线射出,求玻璃体的最大半径。
。不考虑光在AD和BC面上的反射,AB面上都有光线射出,求玻璃体的最大半径。