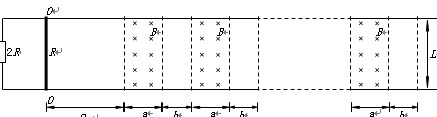
如图所示,两根相距为L的金属轨道固定于水平面上,导轨电阻不计;一根质量为m、长为L、电阻为R的金属棒两端放于导轨上,导轨与金属棒间的动摩擦因数为μ,棒与导轨的接触电阻不计。导轨左端连有阻值为2R的电阻。轨道平面上有n段竖直向下的宽度为a、间距为b的匀强磁场(a>b),磁感应强度为B。金属棒初始位于OO’处,与第一段磁场相距2a。求:
(1)若金属棒有向右的初速度v0,为使金属棒保持v0的速度一直向右穿过各磁场,需对金属棒施加一个水平向右的拉力。求金属棒不在磁场中受到的拉力F1和在磁场中受到的拉力F2的大小;
(2)在(1)的情况下,求金属棒从OO’开始运动到刚离开第n段磁场过程中,拉力所做的功;
(3)若金属棒初速度为零,现对其施以水平向右的恒定拉力F,使棒刚进入各磁场时的速度都相同,求金属棒从OO’开始运动到刚离开第n段磁场整个过程中导轨左端电阻上产生的热量。