如图所示,一水平传送带始终保持着大小为v0=4m/s的速度做匀速运动。在传送带右侧有一半圆弧形的竖直放置的光滑圆弧轨道,其半径为R=0.2m,半圆弧形轨道最低点与传送带右端B衔接并相切,一小物块无初速地放到皮带左端A处,经传送带和竖直圆弧轨道至最高点C。已知当A、B之间距离为s=1m时,物块恰好能通过半圆轨道的最高点C,(g=10m/s2)则: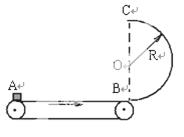
(1)物块至最高点C的速度v为多少?
(2)物块与皮带间的动摩擦因数为多少?
(3)若只改变传送带的长度,使滑块滑至圆弧轨道的最高点C 时对轨道的压力最大,传送带的长度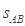 应满足什么条件?
应满足什么条件?
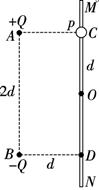
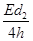 ,电子的重力忽略不计,求:
,电子的重力忽略不计,求: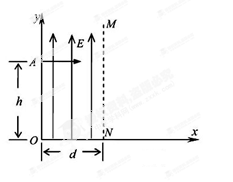


 t图像如图(乙)所示。取重力加速度为g="10" m/s2。求:
t图像如图(乙)所示。取重力加速度为g="10" m/s2。求: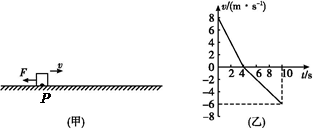
 粤公网安备 44130202000953号
粤公网安备 44130202000953号