如图所示,A、B是静止在光滑水平地面上相同的两块长木板,长度均为L= 0.75m,A的左端和B的右端接触,两板的质量均为M=2.0kg。C是一质量为m=l.0kg的小物块,现给它一初速度v0=2.0m/s,使它从B板的左端开始向右滑动。已知C与A、B之间的动摩擦因数均为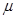 =0.20,最终C与A保持相对静止。取重力加速度g=l0
=0.20,最终C与A保持相对静止。取重力加速度g=l0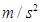 ,求木板A、B最终的速度分别是多少?
,求木板A、B最终的速度分别是多少?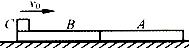
如图所示,A、B是静止在光滑水平地面上相同的两块长木板,长度均为L= 0.75m,A的左端和B的右端接触,两板的质量均为M=2.0kg。C是一质量为m=l.0kg的小物块,现给它一初速度v0=2.0m/s,使它从B板的左端开始向右滑动。已知C与A、B之间的动摩擦因数均为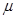 =0.20,最终C与A保持相对静止。取重力加速度g=l0
=0.20,最终C与A保持相对静止。取重力加速度g=l0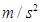 ,求木板A、B最终的速度分别是多少?
,求木板A、B最终的速度分别是多少?