在一个底面积为200cm2、高度为20cm的圆柱形薄壁玻璃容器底部,放入一个边长为10cm的实心正方体物块,然后逐渐向容器中倒入某种液体。图18反映了物块对容器底部压力的大小F与容器中倒入液体的深度h(0~6cm)之间的关系。求: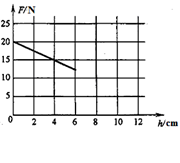
(1)物块的重力;
(2)液体的密度大小;
(3)当倒入液体的深度h为11cm时,物块对容器底部的压强。
推荐套卷
在一个底面积为200cm2、高度为20cm的圆柱形薄壁玻璃容器底部,放入一个边长为10cm的实心正方体物块,然后逐渐向容器中倒入某种液体。图18反映了物块对容器底部压力的大小F与容器中倒入液体的深度h(0~6cm)之间的关系。求:
(1)物块的重力;
(2)液体的密度大小;
(3)当倒入液体的深度h为11cm时,物块对容器底部的压强。