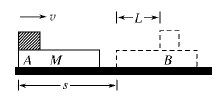
如图所示，AKD为竖直平面内固定的光滑绝缘轨道，轨道间均平滑连接，AK段水平，其间分布有一水平向右的匀强电场I。PQ为同一竖直面内的固定光滑水平轨道。自D点向右宽度L=0.7m的空间，分布有水平向右、场强大小E=1.4×105N/C的匀强电场II。质量m2=0.1kg、长度也为L的不带电绝缘平板，静止在PQ上并恰好处于电场II中，板的上表面与弧形轨道相切于D点。AK轨道上一带正电的小物体从电场I的左边界由静止开始运动，并在D点以速度v=1m/s滑上平板。已知小物体的质量m1=10－2kg，电荷量q=＋10－7C,与平板间的动摩擦因数
,AK与D点的垂直距离为h=0.3m，小物体离开电场II时速度比平板的大、小物体始终在平板上。设小物体电荷量保持不变且视为质点，取g=10m/s2。求：
（1）电场I左右边界的电势差；
（2）小物体从离开电场II开始，到平板速度最大时，所需要的时间。
已知锌的逸出功W0="3.34" eV，试通过计算说明：用波长λ=0.2μm的光照射锌板时能否发生光电效应。(普朗克常量h=6.63×10－34 J·s，真空中光速c=3×108m/s)
如图所示，平行玻璃板的厚度d=4cm，光线AB以入射角i=60°从空气射到平行玻璃板的上表面，经两次折射后从玻璃板的下表面射出。已知玻璃的折射率n=
。求出射光线CD相对于入射光线AB偏离的距离。
铁的密度ρ=7.8×103kg/m3、摩尔质量M=5.6×10-2kg/mol，阿伏加德罗常数
NA=6.0×1023mol-1。铁原子视为球体，估算铁原子的直径大小。（保留一位有效数字）
光滑水平面上放有如图所示的用绝缘材料制成的“┙”型滑板，（平面部分足够长），质量为4m，距滑板的A壁为L1距离的B处放有一质量为m，电量为+q的大小不计的小物体，小物体与板面的摩擦不计，整个装置处于场强为E的匀强电场中，初始时刻，滑板与小物体都静止，试求：
释放小物体，第一次与滑板A壁碰前小物体的速度v1多大？
若小物体与A壁碰后相对水平面的速度大小为碰前的
，则小物体在第二次跟A壁碰撞之前瞬时，滑板的速度v和物体的速度v2分别为多大？（均指对地速度）小物体从开始运动到第二次碰撞前，电场力做功为多大？（碰撞时间可忽略）
粤公网安备 44130202000953号