如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)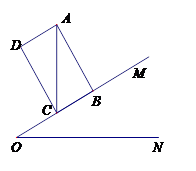
相关知识点
推荐套卷
如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)