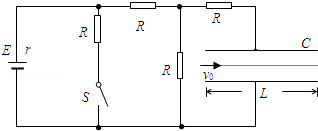
如图所示,一固定斜面体,其斜边与水平底边的夹角 ,BC为一段光滑圆弧轨道,DE为半圆形光滑轨道,两圆弧轨道均固定于竖直平面内,一滑板静止在光滑的地面上,右端紧靠C点,上表面所在平面与两圆弧分别相切于C、D两点。一物块被轻放在斜面上F点由静止释放,物块离开斜面后恰好在B点沿切线进入BC段圆弧轨道,再经C点滑上滑板,滑板运动到D点时被牢固粘连。物块可视为质点,质量为m,滑板质量M=2m,DE半圆弧轨道和BC圆弧轨道的半径均为R,斜面体水平底边与滑板上表面的高度差
,BC为一段光滑圆弧轨道,DE为半圆形光滑轨道,两圆弧轨道均固定于竖直平面内,一滑板静止在光滑的地面上,右端紧靠C点,上表面所在平面与两圆弧分别相切于C、D两点。一物块被轻放在斜面上F点由静止释放,物块离开斜面后恰好在B点沿切线进入BC段圆弧轨道,再经C点滑上滑板,滑板运动到D点时被牢固粘连。物块可视为质点,质量为m,滑板质量M=2m,DE半圆弧轨道和BC圆弧轨道的半径均为R,斜面体水平底边与滑板上表面的高度差 ,板长l=6.5R,板左端到D点的距离L在
,板长l=6.5R,板左端到D点的距离L在 范围内取值,F点距A点的距离s=12.5R,物块与斜面、物块与滑板间的动摩擦因数均为
范围内取值,F点距A点的距离s=12.5R,物块与斜面、物块与滑板间的动摩擦因数均为 ,重力加速度取g。已知sin37°=0.6,cos37°=0.8。求:(结果用字母m、g、R、L表示)
,重力加速度取g。已知sin37°=0.6,cos37°=0.8。求:(结果用字母m、g、R、L表示)
(1)求物块滑到A点的速度大小;
(2)求物块滑到C点时所受圆弧轨道的支持力的大小;
(3)试讨论物块从滑上滑板到离开左端的过程中,克服摩擦力做的功Wf与L的关系;并判断物块能否滑到DE轨道的中点。
相关知识点


 粤公网安备 44130202000953号
粤公网安备 44130202000953号