下图是用传送带传送行李的示意图。图中水平传送带AB间的长度为8m，它的右侧是一竖直的半径为0.8m的1/4圆形光滑轨道，轨道底端与传送带在B点相切。若传送带向右以6m/s的恒定速度匀速运动，当在传送带的左侧A点轻轻放上一个质量为4kg的行李箱时，箱子运动到传送带的最右侧如果没被捡起，能滑上圆形轨道，而后做往复运动直到被捡起为止。已知箱子与传送带间的动摩擦因数为0.1，重力加速度大小为g=10m/s2，求：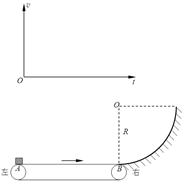
⑴箱子从A点到B点所用的时间及箱子滑到圆形轨道底端时对轨道的压力大小；
⑵若行李箱放上A点时给它一个5m/s的水平向右的初速度，到达B点时如果没被捡
起，则箱子离开圆形轨道最高点后还能上升多大高度？在给定的坐标系中定性画出箱子从A点到最高点过程中速率v随时间t变化的图象。
某汽车司机看到交通岗的绿灯亮后，立即以3m/s2的加速度开始起动汽车，去追赶前方x0=330m远、同方向行驶的自行车．设汽车能达到的最大速度为vm=30m/s，自行车以v1=6m/s的速度做匀速直线运动．试求：汽车在追上自行车前运动多长时间与自行车相距最远？此时他们之间的距离是多少？
汽车至少要用多长时间才能追上自行车?
如图所示，用一根绳子
把物体挂起来，再用一根水平的绳子
把物体拉向一旁固定起来. 物体的重量是40N，绳子与竖直方向的夹角
30°，绳子和对物体的拉力分别是多大？ （答案可保留根号）
如图所示，在以坐标原点O为圆心，半径为R的半圆形区域内，有相互垂直的匀强电场和匀强磁场，磁感应强度为B，磁场方向垂直于xOy平面向里。一带正电的粒子（不计重力）从O点沿y轴正方向以某一速度射人，带电粒子恰好做匀速直线运动，经t0时间从P点射出。
（1）电场强度的大小和方向。
（2）若仅撤去磁场，带电粒子仍从O点以相同的速度射入，经t0/2 时间恰从半圆形区域的边界射出，求粒子运动加速度大小。
（3）若仅撤去电场，带电粒子仍从O点射入但速度为原来的4倍，求粒子在磁场中运动的时间。
如图所示，金属条的左侧有垂直纸面向里的磁感应强度为B、面积足够大的匀强磁场.在金属条正上方，与A点相距上方l处有一涂有荧光材料的金属小球P(半径可忽略).一强光束照射在金属条的A处，可以使A处向各个方向逸出不同速度的电子，小球P因受到电子的冲击而发出荧光.已知电子的质量为m、电荷量为e. 
（1）从A点垂直金属条向左垂直射入磁场的电子中，能击中小球P的电子的速度是多大？
(2) 若A点射出的、速度沿纸面斜向下方，且与金属条成θ角的电子能击中小球P，请导出其速率v与θ的关系式，并在图中画出其轨迹.
粤公网安备 44130202000953号