已知某半径为r0的质量分布均匀的天体,测得它的一个卫星的圆轨道的半径为r,卫星运行的周期为T。假设在该天体表面沿竖直方向以初速度v0向上抛出一个物体,不计阻力,求它可以到达的最大高度h是多少?( )
A.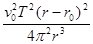 |
B.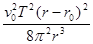 |
C.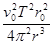 |
D.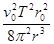 |
已知某半径为r0的质量分布均匀的天体,测得它的一个卫星的圆轨道的半径为r,卫星运行的周期为T。假设在该天体表面沿竖直方向以初速度v0向上抛出一个物体,不计阻力,求它可以到达的最大高度h是多少?( )
A.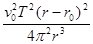 |
B.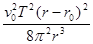 |
C.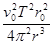 |
D.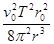 |