如图所示,竖直平面内有一直角坐标系XOY,X轴的正半轴为光滑绝缘水平轨道,负半轴没有轨道,BCP三点都在X轴上,直线MB与Y轴平行,PQ是一个竖直屏。Y轴右边有水平向左的匀强电场E1,MB左边有水平向上的匀强电场E2,MB和Y轴间没有电场;MB右边和圆C内有垂直纸面向外磁感应强度为B的匀强磁场(电场和磁场都没有画出)。一个带正电的小球从A点静止释放,沿直线AB进入圆形磁场。已知:①圆C的半径为 ;②小球的电荷量为q,质量为m;③重力加速度为g;④
;②小球的电荷量为q,质量为m;③重力加速度为g;④  ;⑤ PC间的距离是
;⑤ PC间的距离是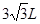 ; ⑥
; ⑥ 。求:
。求:
(1)A点的坐标。
(2)小球打到屏PQ上的点到P点的距离。
(3)当小球离开圆形磁场瞬间,保特原有的条件不变,再在MB左边加一个新的方向与X负半轴方向成30°斜向左下的匀强电场E3,小球刚好垂直打到屏PQ上,求E3的大小
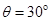 ,其上、下两端点A、B间的距离是3.84m.传送带在电动机的带动下,以4.0m/s顺时针匀速运转.现将质量为10kg的工件(可视为质点)轻放于传送带的A点,已知工件与传送带间的动摩擦因数为
,其上、下两端点A、B间的距离是3.84m.传送带在电动机的带动下,以4.0m/s顺时针匀速运转.现将质量为10kg的工件(可视为质点)轻放于传送带的A点,已知工件与传送带间的动摩擦因数为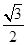 ,则在传送带将工件从A点传送到B点过程中,
,则在传送带将工件从A点传送到B点过程中,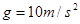 ;求:
;求: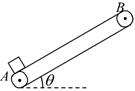
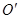 点,另一端系一质量
点,另一端系一质量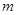 的小球,小球可视为质点。将轻绳拉至水平并将小球由位置A静止释放,小球运动到最低点时,轻绳刚好被拉断。
的小球,小球可视为质点。将轻绳拉至水平并将小球由位置A静止释放,小球运动到最低点时,轻绳刚好被拉断。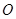 点为顶点的固定斜面,倾角
点为顶点的固定斜面,倾角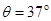 ,斜面足够长,且
,斜面足够长,且 ,已知重力加速度为
,已知重力加速度为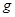 ,忽略空气阻力;求:
,忽略空气阻力;求: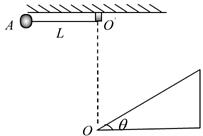
 的小球,以初速度
的小球,以初速度 沿轨道向上运动,求:
沿轨道向上运动,求:
 大小可调节,小球在运动过程中出现脱轨现象,则
大小可调节,小球在运动过程中出现脱轨现象,则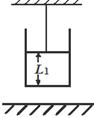
 .一质量也为m的小球A从左侧的最高点自由滑下,A滑到水平面与B碰后立即粘在一起结合成D就不再分离(碰撞时间极短).当D、C一起刚要滑到右侧最低点时,弹簧锁定解除且立即将C弹出并与弹簧分离.求
.一质量也为m的小球A从左侧的最高点自由滑下,A滑到水平面与B碰后立即粘在一起结合成D就不再分离(碰撞时间极短).当D、C一起刚要滑到右侧最低点时,弹簧锁定解除且立即将C弹出并与弹簧分离.求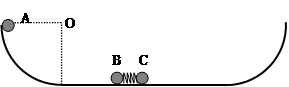
 粤公网安备 44130202000953号
粤公网安备 44130202000953号