如图所示，MNPQ是一块截面为正方形的玻璃砖，其边长MN="30" cm。一束激光AB射到玻璃砖的MQ面上（入射点为B）进入玻璃砖后在QP面上的F点（图中未画出）发生全反射，恰沿DC方向射出。其中B为MQ的中点，∠ABM=30°，PD="7.5" cm，∠CDN=30°。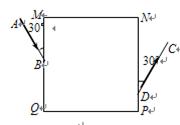
（i）画出激光束在玻璃砖内的光路示意图，求出QP面上的反射点F到Q点的距离QF；
（ii）求出该玻璃砖的折射率；
如图所示，在光滑水平面上使滑块A以2 m/s的速度向右运动，滑块B以4 m/s的速度向左运动并与滑块A发生碰撞，已知滑块A、B的质量分别为1 kg、2 kg，滑块B的左侧连有轻弹簧，求：
（1）当滑块A的速度减为0时，滑块B的速度大小；
（2）弹簧的最大弹性势能．
如图所示，为玻璃材料制成的一棱镜的截面图，一细光束从圆弧AB的中点E点沿半径射入棱镜后，恰好在圆心O点发生全反射，经CD面反射，再从圆弧的F点射出，已知，OA=a，OD=
．求:出射光线与法线夹角的正弦值。
一横截面积为S的内壁光滑的导热汽缸水平放置且固定不动。两个活塞A和B将汽缸分隔为1、2两气室，达到平衡时1、2两气室的体积分别为V1和V2，压强为p0，如图所示。在室温不变的条件下，缓慢推动活塞A，使之向右移动一段距离d后达到新的平衡，活塞移动达到新的平衡后，求：
①汽缸内气体的压强；
②活塞B向右移动的距离。
如图所示，水平放置的轻质弹簧左端与竖直墙壁相连，右侧与质量
的小物块甲相接触但不粘连，B点为弹簧自由端，光滑水平面AB与倾角
的倾斜面BC在B处平滑连接，OCD在同一条竖直线上，CD右端是半径
的
光滑圆弧，斜面BC与圆弧在C处也平滑连接，物块甲与斜面BC间的动摩擦因数
。现用力将物块甲缓慢向左压缩弹簧，使弹簧获得一定能量后撤去外力，物块甲刚好能滑到C点，与此同时用长
的细线悬挂于O点的小物块乙从图示位置静止释放，
，物块乙到达C点时细线恰好断开且与物块甲发生正碰，碰撞后物块甲恰好对圆弧轨道无压力，物块乙恰好从图中P点离开圆弧轨道，取
，
，求：
（1）撤去外力时弹簧的弹性势能
；
（2）小物块乙的质量M和细线所能承受的最大拉力
；
（3）两物块碰撞过程中损失的能量
；
（4）小物块乙落到水平面上时的速度大小
（保留一位有效数字）。
如图所示，平面直角坐标系第一象限存在竖直向上的匀强电场，距离原点O为3a处有一个竖直放置的荧光屏，荧光屏与x轴相交于Q点，且纵贯第四象限。一个顶角等于30°的直角三角形区域内存在垂直平面向里的匀强磁场，三角形区域的一条直角边ML与y轴重合，且MN被x轴垂直平分。已知ML的长度为6a，磁感应强度为B，电子束以相同的速度v0从LO区间垂直y轴和磁场方向射入直角三角形区域。从y=-2a射入磁场的电子运动轨迹恰好经过原点O，假设第一象限的电场强度大小为E=Bv0，试求：
（1）电子的比荷；
（2）电子束从+y轴上射入电场的纵坐标范围；
（3）从磁场中垂直于y轴射入电场的电子打到荧光屏上距Q点的最远距离。
粤公网安备 44130202000953号