苏州金龙汽车有限公司是一家大型客车生产基地.该公司某型号客车在车型测试时,其在一段平直的公路上匀速行驶5.6km,受到的阻力是3.0×103N,消耗燃油1.2kg(假设燃油完全燃烧).若燃油的热值q=4×107J/kg,求:
(1)客车在这段公路上匀速行驶时克服阻力所做的功.
(2)已知热机效率η=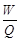 (式中W为热机在某段时间内对外所做的功,Q为它在这段时间内所消耗的燃油完全燃烧所产生的热量),则该车的热机效率是多少?
(式中W为热机在某段时间内对外所做的功,Q为它在这段时间内所消耗的燃油完全燃烧所产生的热量),则该车的热机效率是多少?
相关知识点
推荐套卷
苏州金龙汽车有限公司是一家大型客车生产基地.该公司某型号客车在车型测试时,其在一段平直的公路上匀速行驶5.6km,受到的阻力是3.0×103N,消耗燃油1.2kg(假设燃油完全燃烧).若燃油的热值q=4×107J/kg,求:
(1)客车在这段公路上匀速行驶时克服阻力所做的功.
(2)已知热机效率η=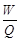 (式中W为热机在某段时间内对外所做的功,Q为它在这段时间内所消耗的燃油完全燃烧所产生的热量),则该车的热机效率是多少?
(式中W为热机在某段时间内对外所做的功,Q为它在这段时间内所消耗的燃油完全燃烧所产生的热量),则该车的热机效率是多少?