如图所示，平行板电容器竖直放置在水平绝缘地板上，一个带电质点质量为m=0.10×10- 3kg，电荷量为q=" -" 2.0×10- 4C，从电容器中心线上某点由静止开始自由下落，下落了h1=0.80m后进入匀强电场，又下落了h2=1.0m后到达水平绝缘地板。落地点在两板中心O点左侧s=20cm处（未碰板）。g取10m/s2。求：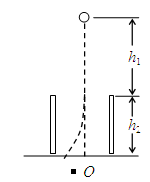
（1）带电质点在空中运动的时间；
（2）电容器中匀强电场的场强E的大小和方向。
在匀强电场中，将一电荷量为2×10-5C的负电荷（仅受电场力作用）由A点移动到B点，其电势能增加了0.1J，已知A,B两点间距为2cm，两点连线与电场方向成600角，如图所示，求：
（1）电荷由A移到B的过程中，电场力做的功W
（2）A,B两点间的电势差为UAB
（3）该匀强电场的场强E
如图21所示，两根金属平行导轨MN和PQ放在水平面上，左端向上弯曲且光滑，导轨间距为L，电阻不计。水平段导轨所处空间有两个有界匀强磁场，相距一段距离不重叠，磁场Ⅰ左边界在水平段导轨的最左端，磁感强度大小为B，方向竖直向上；磁场Ⅱ的磁感应强度大小为2B，方向竖直向下。质量均为m、电阻均为R的金属棒a和b垂直导轨放置在其上，金属棒b置于磁场Ⅱ的右边界CD处。现将金属棒a从弯曲导轨上某一高处由静止释放，使其沿导轨运动。设两金属棒运动过程中始终与导轨垂直且接触良好。
（1）若水平段导轨粗糙，两金属棒与水平段导轨间的最大摩擦力均为
mg，将金属棒a从距水平面高度h处由静止释放。求：
金属棒a刚进入磁场Ⅰ时，通过金属棒b的电流大小；
若金属棒a在磁场Ⅰ内运动过程中，金属棒b能在导轨上保持静止，通过计算分析金属棒a释放时的高度h应满足的条件；
（2）若水平段导轨是光滑的，将金属棒a仍从高度h处由静止释放，使其进入磁场Ⅰ。设两磁场区域足够大，求金属棒a在磁场Ⅰ内运动过程中，金属棒b中可能产生焦耳热的最大值。
回旋加速器是用来加速带电粒子的装置，图中为回旋加速器的示意图。D1、D2是两个中空的铝制半圆形金属扁盒，在两个D形盒正中间开有一条狭缝，两个D形盒接在高频交流电源上。在D1盒中心A处有粒子源，产生的带正电粒子在两盒之间被电场加速后进入D2盒中。两个D形盒处于与盒面垂直的匀强磁场中，带电粒子在磁场力的作用下做匀速圆周运动，经过半个圆周后，再次到达两盒间的狭缝，控制交流电源电压的周期，保证带电粒子经过狭缝时再次被加速。如此，粒子在做圆周运动的过程中一次一次地经过狭缝，一次一次地被加速，速度越来越大，运动半径也越来越大，最后到达D形盒的边缘，沿切线方向以最大速度被导出。已知带电粒子的电荷量为q，质量为m，加速时狭缝间电压大小恒为U，磁场的磁感应强度为B，D形盒的半径为R，狭缝之间的距离为d。设从粒子源产生的带电粒子的初速度为零，不计粒子受到的重力，求：
（1）带电粒子能被加速的最大动能Ek；
（2）带电粒子在D2盒中第n个半圆的半径；
（3）若带电粒子束从回旋加速器输出时形成的等效电流为I，求从回旋加速器输出的带电粒子的平均功率
。
如图19所示，在水平向左、电场强度为E的匀强电场中，竖直固定着一根足够长的粗糙绝缘杆，杆上套着一个质量为m、带有电荷量-q的小圆环，圆环与杆间的动摩擦因数为μ。
（1）由静止释放圆环，圆环沿杆下滑，求圆环下滑过程中受到的摩擦力f；
（2）若在匀强电场E的空间内再加上磁感应强度为B、方向垂直纸面向里的匀强磁场，圆环仍由静止开始沿杆下滑。求：
①圆环刚开始运动时加速度a0的大小；
②圆环下滑过程中的最大动能Ek。
粤公网安备 44130202000953号