在光滑水平桌面中央固定一边长为0.3m的小正三棱柱abc俯视如图所示。长度为L=1m的细线,一端固定在a点,另一端拴住一个质量为m=1kg、不计大小的小球。初始时刻,把细线拉直在ca的延长线上,并给小球以v0=1m/s且垂直于细线方向的水平速度,由于棱柱的存在,细线逐渐缠绕在棱柱上。已知细线所能承受的最大张力为8N,求: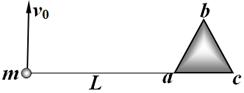
(1)小球从开始运动至绳断时的位移。
(2)绳断裂前小球运动的总时间。
相关知识点
在光滑水平桌面中央固定一边长为0.3m的小正三棱柱abc俯视如图所示。长度为L=1m的细线,一端固定在a点,另一端拴住一个质量为m=1kg、不计大小的小球。初始时刻,把细线拉直在ca的延长线上,并给小球以v0=1m/s且垂直于细线方向的水平速度,由于棱柱的存在,细线逐渐缠绕在棱柱上。已知细线所能承受的最大张力为8N,求: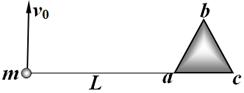
(1)小球从开始运动至绳断时的位移。
(2)绳断裂前小球运动的总时间。