如图，长为L的轻杆一端连着质量为m的小球，另一端用铰链固接于水平地面上的O点，初始时小球静止于地面上，边长为L、质量为M的正方体左侧静止于O点处。现在杆中点处施加一大小始终为12mg/π，方向始终垂直杆的力F，经过一段时间后撤去F，小球恰好能到达最高点。忽略一切摩擦，试求：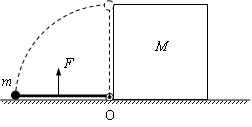
（1）力F所做的功；
（2）力F撤去时小球的速度；
（3）若小球运动到最高点后由静止开始向右倾倒，求杆与水平面夹角为θ时（正方体和小球还未脱离），正方体的速度大小。
如图所示，一个人用一根长为0.5 m的细绳拴一个质量为0.5 kg的小球（可视为质点），使其在竖直平面内做圆周运动，若在某一次实验中小球转至最低点时绳子恰好断了，现测得小球落地点与抛出点间的水平距离为4m。已知圆心O离地面h="2.1" m，
(g取9.8m／s2) 求：
（1）绳子断时小球的速度为多大？
（2）若绳子在最低点断时刚好达到它能承受的最大拉力，求此力。
在沥青铺设的高速公路上，汽车的设计时速是108km/h。若汽车在这种路面上行驶时，轮胎与地面的最大静摩擦力等于车重的0.6.(取g＝10m/s2) 求：
（1）如果汽车在这种高速路上水平转弯，假设弯道的路面是水平的且拐弯时不产生横向滑动，则其弯道的最小半径应是多少？
（2）此高速路上有一圆弧形的拱形立交桥，要使汽车能够不离开地面安全通过圆弧拱桥，这个圆弧拱桥的半径应满足什么条件？
如图15所示，平行金属导轨与水平面间夹角均为θ= 370 ，导轨间距为 lm ，电阻不计，导轨足够长。两根金属棒 ab 和 a’b’的质量都是0.2kg，电阻都是 1Ω ，与导轨垂直放置且接触良好，金属棒a’b’和导轨之间的动摩擦因数为0.5 ，金属棒ab和导轨无摩擦，导轨平面PMKO处存在着垂直轨道平面向上的匀强磁场，导轨平面PMNQ处存在着沿轨道平面向上的匀强磁场，磁感应强度 B 的大小相同．让a’ b’固定不动，将金属棒ab 由静止释放，当 ab 下滑速度达到稳定时，整个回路下滑速度达到稳定时，整个回路消耗的电功率为 18W 。求 ：
( 1 ) ab 达到的最大速度多大？
( 2) ab 下落了 30m 高度时，其下滑速度已经达到稳定，则此过程中回路电流的发热量 Q 多大？
( 3) 在ab下滑过程中某时刻将 a ' b’固定解除，为确保a ' b’始终保持静止，则a ' b’固定解除时ab棒的速度有何要求？ ( g ="10m" / s2 , sin370 ="0.6" ,cos370 ="0.8" )
如图14所示，竖直平面内有一边长为L、质量为m，电阻为R的正方形线框在竖直向下的匀强重力场和水平方向的磁场组成的复合场以初速度v0水平抛出（忽略空气阻力）。运动过程中正方形线框始终在磁场中运动且磁场方向与线框平面始终垂直，磁场的磁感应强度随水平向右的x轴按B=B0+kx的规律均匀增大。（已知重力加速度为g）求：
（1）线框水平方向速度为v1时,线框中瞬时电流的大小；
（2）线框在复合场中运动经时间t，此时速度为v2求此时电功率。
粤公网安备 44130202000953号