如图所示，离子发生器发射一束质量为m，电荷量为+q的离子，从静止经PQ两板间的加速电压加速后，以初速度v0再从a点沿ab方向进入一匀强电场区域，abcd所围成的正方形区域是该匀强电场的边界，已知正方形的边长为L，匀强电场的方向与ad边平行且由a指向d．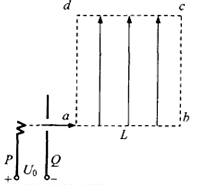
（1）若离子恰从c点飞离电场，求ac两点间的电势差Uac；
（2）若离子从abcd边界上某点飞出时的动能为mv02，求此时匀强电场的场强大小E．
如图所示为小型旋转电枢式交流发电机的原理图，其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动，线圈的匝数n＝100，总电阻r＝10 Ω，线圈的两端经集流环与阻值为R＝90 Ω的电阻R连接，与R并联的交流电压表为理想电表。在t＝0时刻，线圈平面与磁场方向平行，穿过每匝线圈的磁通量Φ随时间t按图乙所示正弦规律变化。求：
(1)交流发电机产生的电动势的最大值；
(2)电路中交流电压表的示数.
如图所示 ，粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接，斜面倾角 θ = 37°，A、C、D滑块的质量为 mＡ= mＣ= mD=" m" =" 1" kg，B滑块的质量 mB =" 4" m =" 4" kg(各滑块均视为质点
)。A、B间夹着质量可忽略的火药。K为处于原长的轻质弹簧，两端分别连接住B和C。现点燃火药（此时间极短且不会影响各物体的质量和各表面的光滑程度），此后，发现A与D相碰后粘在一起，接着沿斜面前进了L =" 0.8" m 时速度减为零，此后设法让它们不再滑下。已知滑块A、D与斜面间的动摩擦因数均为 μ = 0.5，取 g = 10 m/s2，sin37°= 0.6，cos37°= 0.8。求：
（1）火药炸完瞬间A的速度vA；
（2）滑块B、C和弹簧K构成的系统在相互作用过程
中，弹簧的最大弹性势能Ep。(弹簧始终未超出弹性限度)。
一质量为M =" 0.8" kg的中空的、粗细均匀的、足够长的绝缘细管，其内表面粗糙、外表面光滑；有一质量为m =" 0.2" kg、电荷量为q =" 0.1" C的带正电小滑块以水平向右的速度进入管内，如图甲。细管置于光滑的水平地面上，细管的空间能让滑块顺利地滑进去，示意图如图乙。运动过程中滑块的电荷量保持不变。空间中存在垂直纸面向里的水平匀强磁场，磁感强度为B =" 1.0" T。（取水平向右为正方向，g =" 10" m/s2）
(1)滑块以v0 = 10 m/s的初速度进入管内，则系统最终产生的内能为多少?
(2)滑块最终的稳定速度 vt取决于滑块进入细管时的初速度v0，请以滑块的初速度v0为横坐标、滑块最终稳定时的速度vt 为纵坐标，在丙图中画出滑块的vt—v0图象（只需画出v0的取值范围在0至60 m/s的图象）。
一辆长为l1 =" 14" m的客车沿平直公路以v1 =" 8" m/s的速度匀速向东行驶，一辆长为l2 =" 10" m的货车由静止开始以a =" 2" m/s2的加速度由东向西匀加速行驶，已知货车刚启动时两车前端相距s0 =" 240" m
，当货车的速度达到v2 =" 24" m/s时即保持该速度匀速行驶，求两车错车所用的时间。
用单位长度质量
为m、单位长度电阻为r的薄金属条制成边长为L的闭合正方形框
。如图所示，金属方框水平放在磁极的狭缝间，方框平面与磁场方向平行。设匀强磁场仅存在于异名相对磁极的狭缝间，其它地方的磁场忽略不计。可认为方框的
边和
边都处在磁极之间。将方框从静止开始释放，在下落过程中其平面始终保持水平（不计空气阻力）。方框下落的最大速度为vm。
（1）求磁极狭缝间磁感应强度B的大小（设磁场区域在竖直方向足够长）；
（2）当方框下落的加速度为
时，求方框的发热功率P；
（3）已知方框下落时间为t时，下落高度为h，其速度为vt（vt<vm）。若在同一时间t内，方框内产生的热量与某恒定电流I0在该框内产生的热量相同，求恒定电流I0的表达式。
粤公网安备 44130202000953号