有一玻璃半球,右侧面镀银,光源S就在其对称轴SO上(O为球心),且SO水平,如下图所示。从光源S发出的一束光射到球面上,其中一部分光经球面反射后恰能竖直向上传播,另一部分光折入玻璃半球内,经右侧镀银面第一次反射恰能沿原路返回。若球面半径为R,玻璃折射率为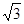 ,求光源S与球心O之间的距离SO为多大?
,求光源S与球心O之间的距离SO为多大?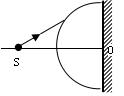
有一玻璃半球,右侧面镀银,光源S就在其对称轴SO上(O为球心),且SO水平,如下图所示。从光源S发出的一束光射到球面上,其中一部分光经球面反射后恰能竖直向上传播,另一部分光折入玻璃半球内,经右侧镀银面第一次反射恰能沿原路返回。若球面半径为R,玻璃折射率为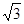 ,求光源S与球心O之间的距离SO为多大?
,求光源S与球心O之间的距离SO为多大?