在如图所示的电路中,已知电源电动势E="3" V,内电阻r=1Ω,电阻R1=2Ω,滑动变阻器R的阻值可连续增大,问: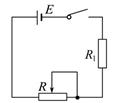
（1）当R多大时,R消耗的功率最大?最大功率为多少? 当R消耗功率最大时电源的效率是多少？
（2）当R多大时,R1消耗的功率最大?最大功率为多少?
（3）当R为多大时，电源的输出功率最大？最大为多少？
如图所示，坐标平面的第Ⅰ象限内存在大小为E、方向水平向左的匀强电场，第Ⅱ象限内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场。足够长的挡板MN垂直x轴放置且距原点O的距离为d。一质量为m、带电量为-q的粒子若自距原点O为L的A点第一次以大小为v0，方向沿y轴正方向的速度进入磁场，则粒子恰好到达O点而不进入电场。现该粒子仍从A点第二次进入磁场，但初速度大小为2v0，为使粒子进入电场后能垂直打在挡板上，求粒子（不计重力）在A点第二次进入磁场时：
（1）其速度方向与x轴正方向之间的夹角。
（2）粒子到达挡板上时的速度大小及打到挡板MN上的位置到x轴的距离.
体育课上进行“爬杆”活动，使用了一根质量忽略不计的长杆，竖直固定，（如图）。一质量为40kg的同学（可视为质点）爬上杆的顶端后，自杆顶由静止开始先匀加速再匀减速下滑，滑到竹杆底端时速度刚好为零．通过装在长杆底部的传感器测得长杆对底座的最大压力为4
60N，最小压力280N，下滑的总时间为3s，求该杂技演员在下滑过程中的最大速度及杆的长度。（
）
质量
的物体在方向平行于斜面、大小为
的拉力作用下，从固定粗糙斜面的底端由静止开始沿斜面向上运动，拉力
作用
后撤去。已知斜面与水平面的夹角
，如图所示。斜面足够长，物体与斜面间的动摩擦因数
，取重力加速度
。求：
（1）在拉力作用下，物体的加速度大小
（2）撤去拉力后，物体沿斜面向上滑行的时间
（3）自静止开始到上
滑至速度为零时，物体通过的总位移大小
（
，
）
如图所示，质量m＝1 kg的小球用细线拴住，线长l＝0.5 m，细线所受拉力达到F＝18 N时就会被拉断.当小球从图示位置释放后摆到悬点的正下方时，细线恰好被拉断。若此时小球距水平地面的高度h＝5 m，重力加速度g＝10
m/s2，求小球落地处到地面上Ｐ点的距离.（P点在悬点的正下方）
，用与竖直方向成
的斜向右上方的推力
把该物体压在竖直墙壁上，并使它沿墙壁在竖直方向上做匀速直线运动。物体与墙壁间的动摩擦因数
，取重力加速度
，求推力
，
）
粤公网安备 44130202000953号