（本题8分）一个不透明的口袋装有若干个红、黄、蓝、绿四种颜色的小球，小球除颜色外完全相同，为估计该口袋中四种颜色的小球数量，每次从口袋中随机摸出一球记下颜色并放回，重复多次试验，汇总实验结果绘制如图不完整的条形统计图和扇形统计图．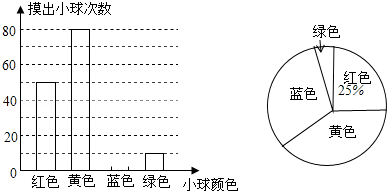
根据以上信息解答下列问题：
（1）求实验总次数，并补全条形统计图；
（2）扇形统计图中，摸到黄色小球次数所在扇形的圆心角度数为多少度？
（3）已知该口袋中有10个红球，请你根据实验结果估计口袋中绿球的数量．
（11·丹东）（本题8分）每个小方格是边长为1个单位长度的小正方形，梯形ABCD在平面直角坐标系中的位置如图所示.
（1）在平面直角坐标系中画出梯形ABCD关于直线AD的轴对称图形AB1C1D；
（2）点P是
轴上一个动点，请直接写出所有满足△POC是等腰三角形的动点P的坐标.
（11·大连）（本题12分）如图15，抛物线y＝ax2＋bx＋c经过A (－1，0)、B (3，
0)、C (0，3)三点，对称轴与抛物线相交于点P、与直线BC相交于点M，连接PB．
（1）求该抛物线的解析式；
（2）抛物线
上是否存在一点Q，使△QMB与△PMB的面积相等，若存在，求点Q的坐标；
若不存在，说明理由；
（3）在第一象限、对称轴右侧的抛物线上是否存在一点R，使△RPM与△RMB的面积相
等，若存在，直接写出点R的坐标；若不存在，说明理由．
（11·大连）（本题12分）在△ABC中，∠A＝90°，点D在线段BC上，∠EDB
＝
∠C，BE⊥DE，垂足为E，DE与AB相交于点F．
（1）当AB＝AC时，（如图13），
① ∠EBF＝_______°；
② 探究线段BE与FD的数量关系，并加以证明；
（2）当AB＝kAC时（如图14），求
的值（用含k的式子表示）．
（11·大连）（本题11分）如图，在平面直角坐标系中，点A、B、C的坐标分别
为(0，2)、(－1，0)、(4，0)．P是线段OC上的一动点（点P与点O、C不重合），过点P
的直线x＝t与AC相交于点Q
．设四边形ABPQ关于直线x＝t的对称的图形与△QPC重叠
部分的面积为S．
（1）点B关于直线x＝t的对称点B′的坐标为________；
（2）求S与t的函数关系式．
（容器各面的厚
粤公网安备 44130202000953号