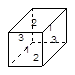有8个棱长是1的小正方体，每个小正方体有三组相对的面，第一组相对的面上都写着数字1，第二组相对的面上都写着数字2，第三组相对的面上都写着数字3(如图)．现在把这8个小正方体拼成一个棱长是2的大正方体.。问：是否有一种拼合方式，使得大正方体每一个面上的4个数字之和恰好组成6个连续的自然数?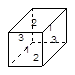 
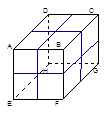
相关试题
有8个棱长是1的小正方体，每个小正方体有三组相对的面，第一组相对的面上都写着数字1，第二组相对的面上都写着数字2，第三组相对的面上都写着数字3(如图)．现在把这8个小正方体拼成一个棱长是2的大正方体.。问：是否有一种拼合方式，使得大正方体每一个面上的4个数字之和恰好组成6个连续的自然数?
+
×76﹣2.4÷
×97
×
+
×
+
÷
×24﹣
．
÷0.6×
÷9+
×
×101﹣
÷
﹣
（
﹣
+
）÷
[1﹣（
+
．
×
2.25×1.8+12.5×0.18[1﹣（
+
）]×36．
+
×25%
÷（1﹣
×
）
）
﹣
）÷（
+
）
×
+
375+450÷18×25
+
﹣
）2﹣
÷
﹣
粤公网安备 44130202000953号