如图所示,固定在竖直平面内半径为R的四分之一光滑圆弧轨道与水平光滑轨道平滑连接,A、B二个滑块质量均为m,B静止在光滑水平轨道上的图示位置。滑块A从圆弧上的P点由静止滑下(P点处半径与水平面成30°角),与B发生正碰并粘合向右运动。求A、B粘合后的速度大小。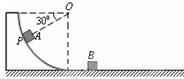
如图所示,固定在竖直平面内半径为R的四分之一光滑圆弧轨道与水平光滑轨道平滑连接,A、B二个滑块质量均为m,B静止在光滑水平轨道上的图示位置。滑块A从圆弧上的P点由静止滑下(P点处半径与水平面成30°角),与B发生正碰并粘合向右运动。求A、B粘合后的速度大小。