(15分)小明用台秤研究人在升降电梯中的超重与失重现象．他在地面上用台秤称得其体重为500 N，再将台秤移至电梯内称其体重，电梯从t＝0时由静止开始运动到t＝11 s时停止，得到台秤的示数F随时间t变化的图象如图所示，g取10 m/s2.求：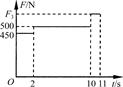
（1）小明在0～2s内加速度a1的大小，并判断在这段时间内他处于超重还是失重状态；
（2）在10～11s内，台秤的示数F3；
（3）小明运动的总位移x.
如图所示，倾角为θ=30°的足够长的固定斜面上，在底端0处固定一垂直斜面的档板，斜面上OM段光滑，M点及以上均粗糙。质量为m的物块A在M点恰好能静止，有一质量为2m的光滑小物块B以初速度
自N点滑向物块A，已知MN=L，AB间每次碰撞后即紧靠在一起但不粘连，每次AB与档板碰撞后均原速率弹回，求：
(1)A、B第一次碰撞后紧靠在一起的初速度
；
(2)物块A在M点上方时，离M点的最大距离s；
(3)系统由于摩擦和碰撞所产生的总内能E。
如图，在xoy直角坐标系中，在第三象限有一平行x轴放置的平行板电容器，板间电压U=1×102V。现有一质量m=1.0×10-12kg，带电量q=2.0×10-10C的带正电的粒子(不计重力)，从下极板处由静止开始经电场加速后通过上板上的小孔，垂直x轴从A点进入第二象限的匀强磁场中。磁场方向垂直纸面向外，磁感应强度B=1T。粒子在磁场中转过四分之一圆周后又从B点垂直y轴进入第一象限，第一象限中有平行于y轴负方向的匀强电场E，粒子随后经过x轴上的C点，已知OC=1m。求：
(1)粒子在磁场中做匀速圆周运动的半径r。
(2)第一象限中匀强电场场强E的大小。
【2012• 湖南模拟】如图所示，处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距
，导轨平面与水平面成θ=37°角，下端连接阻值为
的电阻。匀强磁场大小
、方向与导轨平面垂直．质量为
、电阻
的金属棒放在两导轨上，棒与导轨垂直并保持良好接触，它们之间的动摩擦因数为0.25（已知
，
，取g＝10m／s2) 。
(1)求金属棒沿导轨由静止开始下滑时的加速度大小；
(2)求金属棒稳定下滑时的速度大小及此时ab两端的电压Uab为多少；
(3)当金属棒下滑速度达到稳定时，机械能转化为电能的效率是多少（保留2位有效数字）。
【2012• 北京市西城区期末】如图所示，光滑金属直轨道MN和PQ固定在同一水平面内，MN、PQ平行且足够长，两轨道间的宽度L＝0.50m。轨道左端接一阻值R=0.50Ω的电阻。轨道处于磁感应强度大小B＝0.40T，方向竖直向下的匀强磁场中。质量m=0.50kg的导体棒ab垂直于轨道放置。在沿着轨道方向向右的力F作用下，导体棒由静止开始运动，导体棒与轨道始终接触良好并且相互垂直。不计轨道和导体棒的电阻，不计空气阻力。
（1）若力F的大小保持不变，且F=1.0N。求
a．导体棒能达到的最大速度大小vm；
b．导体棒的速度v=5.0m/s时，导体棒的加速度大小a。
（2）若力F的大小是变化的，在力F作用下导体棒做初速度为零的匀加速直线运动，加速度大小a=2.0m/s2。从力F作用于导体棒的瞬间开始计时，经过时间t=2.0s，求力F的冲量大小I。
【2012•浙江台州市高期末质量评估】如图（甲）
所示，M1M4、N1N4为平行放置的水平金属轨道，M4P、N4Q为相同半径，平行放置的竖直半圆形金属轨道，M4、N4为切点，P、Q为半圆轨道的最高点，轨道间距L=1.0m，圆轨道半径r=0.32m，整个装置左端接有阻值R=0.5Ω的定值电阻。M1M2N2N1、M3M4N4N3为等大的长方形区域Ⅰ、Ⅱ，两区域宽度 d=0.5m，两区域之间的距离s=1.0m；区域Ⅰ内分布着均匀的变化的磁场B1，变化规律如图（乙）所示，规定竖直向上为B1的正方向；区域Ⅱ内分布着匀强磁 场B2，方向竖直向上。两磁场间的轨道与导体棒CD间的动摩擦因数为μ=0.2，M3N3右侧的直轨道及半圆形轨道均光滑。质量m=0.1kg，电阻R0=0.5Ω的导体棒CD在垂直于棒的水平恒力F拉动下，从M2N2处由静止开始运动，到达M3N3处撤去恒力F，CD棒匀速地穿过匀强磁场区，恰好通过半圆形轨道的最高点PQ处。若轨道电阻、空气阻力不计，运动过程导棒与轨道接触良好且始终与轨道垂直，g取10m/s2求：
（1）水平恒力F的大小；
（2）CD棒在直轨道上运动过程中电阻R上产生的热量Q；
（3）磁感应强度B2的大小。
粤公网安备 44130202000953号