如图甲所示，CABAD为竖直放置的轨道，其中圆轨道的半径r＝0.10 m，在轨道的最低点A和最高点B各安装了一个压力传感器(图中未画出)，小球(可视为质点)从斜轨道的不同高度由静止释放，可测出小球在轨道内侧通过这两点时对轨道的压力分别为FA和FB，g取10 m/s2.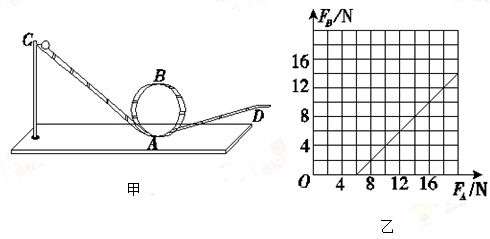
(1)若不计小球所受的阻力，且小球恰好能通过B点，求小球通过A点时速度vA的大小．
(2)若不计小球所受的阻力，小球每次都能通过B点，FB随FA变化的图线如图乙所示，求小球的质量m.
相关试题
如图所示，把质量为0.2克的带电小球A用丝线吊起，若将带电量为4×10-8C的小球B靠近它，当两小球在同一高度时且相距3cm，丝线与坚直方向夹角为45°,求此时小球B受到库仑力及小球A带的电量。
相关知识点
粤公网安备 44130202000953号