如图甲是2012年我国运动员在伦敦奥运会上蹦床比赛中的一个情景。设这位蹦床运动员仅在竖直方向上运动，运动员的脚在接触蹦床过程中，蹦床对运动员的弹力F随时间t的变化规律通过传感器用计算机绘制出来，如图乙所示。取g= 10m/s2，根据F-t图象分析求解：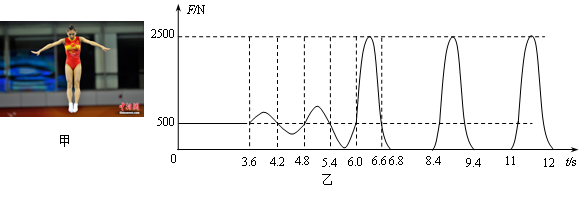
（1）运动员的质量；
（2）运动员在运动过程中的最大加速度；
（3）在不计空气阻力情况下，运动员重心离开蹦床上升的最大高度。
加速性能是汽车的一项重要技术指标。某辆汽车从静止开始加速，经过t="3" s时间速度达到v="15" m/s．在这一加速过程中，汽车的运动可视为匀加速直线运动．求：
（1）该汽车的加速度大小；
（2）6 s内汽车加速运动的位移大小；
（3）第6 s内汽车的平均速率．
如图所示，在水平向右的匀强电场中，有一根长度为
m的绝缘轻细绳，将质量为
kg、电荷量
的带正电小球（可看成质点）悬挂在Q点，绳的悬点为
（绳可绕点自由转动），匀强电场的场强大小
．现将小球拉到右侧与O等高的P点（细绳伸直），以
m/s的初速度竖直向下抛出，当小球下摆至最低点
时，匀强电场方向立即变为竖直向上（场强大小不变），当小球运动到圆周的最高点
时电场立即消失．求：
（1）小球第一次下摆至最低点过程中的最大速率；
（2）小球到达点时的速度大小；
（3）小球第二次到达点时细绳对小球的拉力大小．
（4）电场消失后小球所能达到的最大高度（距离Q点）．
如图所示，质量为m、电荷量为e的电子（初速度为0）经加速电压U1加速后，在水平方向沿O1O2垂直进入偏转电场．已知形成偏转电场的平行板电容器的极板长为L（不考虑电场边缘效应），两极板间距为d，O1O2为两极板的中线，P是足够大的荧光屏，且屏与极板右边缘的距离也为L．
（1）求粒子进入偏转电场的速度v的大小；
（2）若偏转电场两板M、N间加恒定电压
时，电子经过偏转电场后正好打中屏上的A点，A点与极板M在同一水平线上，求的大小．
如图所示，一带电荷量为q=－5×10－3 C，质量为m="0.1" kg的小物块放在一倾角为θ=37°的光滑绝缘斜面上，当整个装置处在一水平向左的匀强电场中时，小物块恰处于静止状态．已知重力加速度g=10m/s2，
，
．
（1）求电场强度E的大小；
（2）某时刻小物块的电荷量突然减少了一半，求物块下滑距离L="1.5" m时的速度大小．
粤公网安备 44130202000953号