如图所示,质量为m的小球用长为L的轻质细线悬于O点,与O点处于同一水平线上的P点处有一个光滑的细钉。已知OP=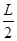 ,在A点给小球一个水平向左的初速度v0,发现小球恰能到达跟P点在同一竖直线上的最高点B,则:
,在A点给小球一个水平向左的初速度v0,发现小球恰能到达跟P点在同一竖直线上的最高点B,则: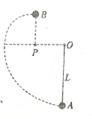
(1)小球到达B点时的速率?
(2)若不计空气阻力,则初速度v0为多少?
(3)若初速度v0= ,则在小球从A到B的过程中克服空气阻力做了多少功?
,则在小球从A到B的过程中克服空气阻力做了多少功?
相关知识点
如图所示,质量为m的小球用长为L的轻质细线悬于O点,与O点处于同一水平线上的P点处有一个光滑的细钉。已知OP=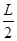 ,在A点给小球一个水平向左的初速度v0,发现小球恰能到达跟P点在同一竖直线上的最高点B,则:
,在A点给小球一个水平向左的初速度v0,发现小球恰能到达跟P点在同一竖直线上的最高点B,则:
(1)小球到达B点时的速率?
(2)若不计空气阻力,则初速度v0为多少?
(3)若初速度v0= ,则在小球从A到B的过程中克服空气阻力做了多少功?
,则在小球从A到B的过程中克服空气阻力做了多少功?