如图，水平地面上的矩形箱子内有一倾角为θ的固定斜面，斜面上放一质量为m的光滑球。静止时，箱子顶部与球接触但无压力。箱子由静止开始向右做匀加速运动，然后改做加速度大小为a的匀减速运动直至静止，经过的总路程为s，运动过程中的最大速度为v．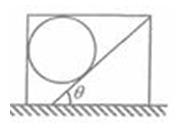
（1）求箱子加速阶段的加速度大小a'。
（2）若a>g tanθ，求减速阶段球受到箱子左壁和顶部的作用力。
如图所示，半径R =" 0.8" m的光滑绝缘导轨固定于竖直平面内，加上某一方向的匀强电场时，带正电的小球沿轨道内侧做圆周运动。圆心O与A点的连线与竖直成一角度θ，在A点时小球对轨道的压力FN="120" N，此时小球动能最大。若小球的最大动能比最小动能多32 J，且小球能够到达轨道上的任意一点（不计空气阻力）。则：
⑴小球的最小动能是多少？
⑵小球受到重力和电场力的合力是多少？
⑶现小球在动能最小的位置突然撤去轨道，并保持其他量都不变，若小球在0.04 s后的动能与它在A点时的动能相等，求小球的质量。
如图所示，跨过轻质定滑轮的细绳两端，一端连接质量为m的物体A，另一端通过一轻质弹簧与质量为M的物体B连接，B物体静止在地面上，用手托着A物体，在A距地面高h处时，细绳刚好被拉直、弹簧无形变。今将A物体从h高处无初速释放，A物体恰好能到达地面，且A到达地面时，B物体对地面的压力恰好减为零。已知重力加速度为g，弹簧的弹性势能与劲度系数k、弹簧的伸长量x的关系是：E弹=
kx2。两个物体均可视为质点，不计绳子和滑轮的质量，不计滑轮轴上的摩擦力和空气阻力。问：
（1）A、B两物体的质量之比为多少?
（2）现将A、B两物体的初始位置互换，再让B物体从h高处无初速释放，当A物体刚要离开地面时，B物体的速度是多少?
物体在距某一行星表面某一高度的O点由静止开始做自由落体运动，依次通过A、B、C三点，已知AB段与BC段的距离相等，均为24 cm，通过AB与BC的时间分别为0.2 s与0.1 s，若该星球的半径为180 km，则环绕该行星的卫星做圆周运动的最小周期为多少？
有两个人要把质量m="1000" kg的货物装进离地h="1" m高的卡车车厢内。他们找来L="5" m的斜面，但没有其他任何工具可用。假设货物在水平地面上和此斜面上滑动时所受摩擦阻力恒为货物重力的0.12倍，两个人的最大推力各为800 N。
（1）通过分析说明俩人能否将货物直接推进车厢？
（2）请你帮助他们设计一个可行的方案，使俩人用最大推力能将货物推进车厢。并详细证明之。（g取10 m/s2）
粤公网安备 44130202000953号