设△ABC的三边长分别为a,b,c,△ABC的面积为S,内切圆半径为r,则r= ,类比这个结论可知:四面体S—ABC的四个面的面积分别为S1,S2,S3,S4,内切球半径为R,四面体S—ABC的体积为V,则R等于
,类比这个结论可知:四面体S—ABC的四个面的面积分别为S1,S2,S3,S4,内切球半径为R,四面体S—ABC的体积为V,则R等于
A. |
B. |
C.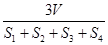 |
D. |
相关知识点
推荐套卷
设△ABC的三边长分别为a,b,c,△ABC的面积为S,内切圆半径为r,则r= ,类比这个结论可知:四面体S—ABC的四个面的面积分别为S1,S2,S3,S4,内切球半径为R,四面体S—ABC的体积为V,则R等于
,类比这个结论可知:四面体S—ABC的四个面的面积分别为S1,S2,S3,S4,内切球半径为R,四面体S—ABC的体积为V,则R等于
A. |
B. |
C.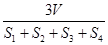 |
D. |