如图所示，水平地面的B点右侧有一圆形挡板。圆的半径R=4m，B为圆心，BC连线与竖直方向夹角为37o．滑块静止在水平地面上的A点，AB间距L=4．5m．现用水平拉力F=18N沿AB方向拉滑块，持续作用一段距离后撤去，滑块恰好落在圆形挡板的C点，已知滑块质量 2kg，与水平面间的动摩擦因数μ=0．4，取g=10m/s2，sin37 o =0．6，cos37 o=0．8．求：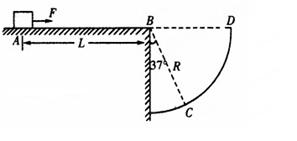
(1)拉力F作用的距离，
(2)滑块从A点运动到圆弧上C点所用的时间．
如图所示，A、B、C是匀强电场中的三点，已知
A="10" V，B ="4" V，C＝－2 V，∠A=30°，∠B=90°，AC=4
cm，试确定：
该电场中的一条电场线．
场强E的大小．
如图所示，a、b、c、d为匀强电场中四个等势面，相邻等势面间距离为2 cm，已知UAC="60" V，求：
电场强度是多大?
设B点电势为零，求A、C、D、P点的电势．
求将q=－1．0×10－10C的点电荷由A移到D电场力所做的功WAD．
将q=2×10－10C的点电荷由B移到C，再经D最后回到P，电场力所做的功WBCDP．
一个钚的同位素Pu的原子核静止在匀强磁场中．某时刻该原子核垂直于磁场方向放射出一个α粒子，变成铀的同位素，同时辐射出能量为E＝0.09 MeV的光子．已知钚原子核的质量M0＝238.999655 u，α粒子的质量m＝4.001509 u，反冲核的质量M＝234.993470 u．取1 u·c2＝931 MeV.
(1)写出衰变的核反应方程．
(2)α粒子和反冲核的动能各是多少？
(3)画出α粒子和反冲核在垂直于纸面向里的匀强磁场中运动轨迹的示意图．
太阳内部持续不断地发生着4个质子聚变为一个氦核的热核反应，这个核反应释放出的大量能量就是太阳的能源．
(1)写出这个核反应方程．
(2)这一核反应能释放出多少能量？
(3)已知太阳每秒释放能量为3.8×1026 J，则太阳每秒减少的质量为多少kg?
(4)若太阳质量减小万分之三，热核反应不能继续进行，计算太阳还能存在多少年？(mp＝1.0073 u，mα＝4.0015 u，me＝0.00055 u，太阳的质量为2×1030 kg)
粤公网安备 44130202000953号