如图所示,在动摩擦因数μ=0.2的水平面上有一质量为m=3kg的物体被一个劲度系数为k="240" N/m的压缩(在弹性限度内)轻质弹簧突然弹开,物体离开弹簧后在水平面上继续滑行了1 m才停下来。已知在弹性限度内弹簧弹性势能为EP=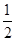 kx2其中k为弹簧的劲度系数,x为弹簧的形变量。(g取10 m/s2)。求:
kx2其中k为弹簧的劲度系数,x为弹簧的形变量。(g取10 m/s2)。求: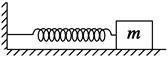
(1)物体开始运动时弹簧的弹性势能
(2)物体最大动能最大时,弹簧的形变量
如图所示,在动摩擦因数μ=0.2的水平面上有一质量为m=3kg的物体被一个劲度系数为k="240" N/m的压缩(在弹性限度内)轻质弹簧突然弹开,物体离开弹簧后在水平面上继续滑行了1 m才停下来。已知在弹性限度内弹簧弹性势能为EP=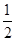 kx2其中k为弹簧的劲度系数,x为弹簧的形变量。(g取10 m/s2)。求:
kx2其中k为弹簧的劲度系数,x为弹簧的形变量。(g取10 m/s2)。求:
(1)物体开始运动时弹簧的弹性势能
(2)物体最大动能最大时,弹簧的形变量