如图xOy平面坐标系，x轴方向为水平方向，y轴方向为竖直方向，在第一象限内有竖直向下的匀强电场E，在第二象限内场强为E的匀强电场与x轴正方向成37°（sin37°=0.6，cos37°=0.8），在（﹣l，l）处一带电荷量为q的带电小球由静止开始沿x轴正方向直线运动，然后进入第一象限．求：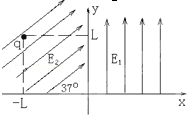
（1）带电小球第一次经过x轴时的位置坐标
（2）带电小球第一次经过x轴是的动能．
如图甲所示，两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上，两导轨间距为l。M、P两点间接有阻值为
R的电阻。一根质量为m的均匀直金属
杆ab放在两导轨上，并与导轨垂直，导轨和金属杆的电阻可忽略。整套装置处于磁感应强度为B的匀强磁场中，磁场方向垂直斜面向下。让ab杆沿导轨由静止开始下滑，导轨和金属杆接触良好，不计它们之间的摩擦，重力加速度为g。
（1）由b向a方向看到的装置如图乙所示，请画出ab杆下滑过程中某时刻的受力示意图；
（2）在加速下滑时，当ab杆的速度大小为υ时，求ab杆中的电流及其加速度的大小；
（3）求在下滑过程中，ab杆可以达到的速度最大值。
一台小型电动机在3 V电压下工作，用此电动机提升所受重力为4 N的物体时，通过它的电流是0.2 A．在30 s内可使该物体被匀速提升3 m．若不计除电动机线圈生热之外的能量损失，求：
(1)电动机的输入功率；
(2)在提升重物的30 s内，电动机线圈所产生的热量；
(3)线圈的电阻．
如图所示，足够长的木板质量
，放置于光滑水平地面上，以初速度
沿水平地面向右匀速运动．现有足够多的小铁块，它们的质量均为m=lkg，在木板上方有一固定挡板，当木板运动到其最右端位于挡板正下方时，将一小铁块贴着挡板无初速地放在木板上，小铁块与木板的上表面间的动摩擦因数
，当木板运动了
时，又无初速地贴着挡板在第1个小铁块上放上第2个小铁块，只要木板运动了
就按同样的方式再放置一个小铁块，直到木板停止运动．(取g=l0m
)，试问：
(1)第1个铁块放上后，木板运动了L时，木板的速度多大?
(2)最终木板上放有多少个铁块?
(3)最后一个铁块放上后，木板再向右运动的距离是多少?
足够长的倾角θ=53°的斜面固定在水平地面上，一物体以v0=6.4m/s的初速度从斜面底端向上滑行，该物体与斜面间的动摩擦因数μ=0.8，如图所示。（sin53°=0.8，cos53°=0.6，g取10m/s2）
⑴求物体从开始到再次返回斜面底端所需的时间；
⑵求返回斜面底端时的速度；
粤公网安备 44130202000953号