半径为R的玻璃半圆柱体，横截面如图所示，圆心为O 。两条平行单色红光沿截面射向圆柱面方向与底面垂直。光线1的入射点A为圆柱面的顶点，光线 2的入射点B，∠AOB＝60°，已知该玻璃对红光的折射率n＝
。求：
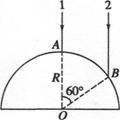
（1）两条光线经柱面和底面折射后出射光线的交点与O点的距离d；
（2）若入射的是单色蓝光，则距离d将比上面求得的结果大还是小？（定性分析，不需要计算，画出光路图）
半径r=0.4m的光滑绝缘轨道固定于竖直平面内，加上某一方向的匀强电场时，带电小球沿轨道内侧做圆周运动，小球动能最大的位置在A点，圆心O与A点的连线与竖直线成一角度如图所示，小球经过A点时，对轨道的压力为N=108N，若小球的最大动能比最小初动能多14.4J，且小球能够到达轨道上任意的一点，试求：
（1）小球的最小动能为多少？
（2）若小球在动能最小位置时突然撤去轨道，并保持其它条件不变，则小球经0.02s时，其动能与A点时的动能相等，小球的质量为多大？
如图：电源电动势E=12V，内阻r=1Ω,R1=3Ω,R2=2Ω,C1=4μFC2=
1μF当S闭合时间足够长时，
求：（1）C1和C2所带电量：
（2）当S断开后，通过R2的电荷量
一根长为l的丝线吊着一质量为m
，带电荷量为q
的小球静止在水平向右的匀强电场中，如图所示丝线与竖直方向成37°角，
现突然将该电场方向变为向下且大小不变，不考虑因电场的改变而带来的其他影响(重力加速度为g)，求
(1)匀强电场的电场强度的大小；
(2)小球经过最低点时丝线的拉力．
质量为m的小物块，用轻弹簧固定在斜面体上，斜面的倾角为
，轻弹簧的劲度系数为k，如图所示．整个装置放在电梯内．
（1）若斜面光滑，电梯静止时弹簧的伸长量为x．如果电梯竖直向上做匀加速直线运动，弹簧的伸长量为2 x．求电梯竖直向上加速运动时的加速度．
（2）若斜面不光滑，斜面与物块之间的动摩擦因数为
，弹簧的伸长量也为2 x，求此时电梯上升加速度的最大值．（设最大静摩擦力与滑动摩擦力大小相等）
的斜面，一名滑雪者总质量m=80kg，他在这段斜坡上从静止开始匀加速下滑50m时，其速度增大到20m/s，（不计空气阻力，取g=10m/s2）问：
粤公网安备 44130202000953号