机械横波某时刻的波形图如图所示,波沿x轴正方向传播,质点p的坐标x=0.32 m.从此时刻开始计时.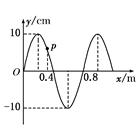
(1)若每间隔最小时间0.4 s重复出现波形图,求波速.
(2)若p点经0.4 s第一次达到正向最大位移,求波速.
(3)若p点经0.4 s到达平衡位置,求波速.
相关知识点
机械横波某时刻的波形图如图所示,波沿x轴正方向传播,质点p的坐标x=0.32 m.从此时刻开始计时.
(1)若每间隔最小时间0.4 s重复出现波形图,求波速.
(2)若p点经0.4 s第一次达到正向最大位移,求波速.
(3)若p点经0.4 s到达平衡位置,求波速.