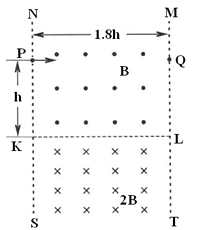
如图所示，在无限长的竖直边界和间充满匀强电场，同时该区域上、下部分分别充满方向垂直于平面向外和和，为上下磁场的水平分界线，在和边界上，距高处分别有两点，和间距为.质量为、带电量为的粒子从点垂直于边界射入该区域，在两边界之间做圆周运动，重力加速度为.
（1）求该电场强度的大小和方向。
（2）要使粒子不从边界飞出，求粒子入射速度的最小值。
（3）若粒子能经过点从边界飞出，求粒子入射速度的所有可能值。
如图所示，PQ和EF为水平放置的平行金属导轨，间距为l＝1.0 m，导体棒ab跨放在导轨上，棒的质量为m＝20 g，棒的中点用细绳经轻滑轮与物体c相连，物体c的质量M＝30 g．在垂直导轨平面方向存在磁感应强度B＝0.2 T的匀强磁场，磁场方向竖直向上，重力加速度g取10 m/s2.若导轨是粗糙的，且导体棒与导轨间的最大静摩擦力为导体棒ab重力的0.5倍，若要保持物体c静止不动，应该在棒中通入多大的电流？电流的方向如何？
一电路如图所示，电源电动势E＝28 V，内阻r＝2 Ω，电阻R1＝12 Ω，R2＝R4＝4 Ω，R3＝8 Ω，C为平行板电容器，其电容C＝3.0 pF，虚线到两极板间距离相等，极板长L＝0.20 m，两极板的间距d＝1.0×10－2m.
(1)若开关S处于断开状态，则当其闭合后，求流过R4的总电荷量为多少？
(2)若开关S断开时，有一带电微粒沿虚线方向以v0＝2.0 m/s的初速度射入C的电场中，刚好沿虚线匀速运动，问：当开关S闭合后，此带电微粒以相同初速度沿虚线方向射入C的电场中，能否从C的电场中射出？(要求写出计算和分析过程，g取10 m/s2)
如图所示，已知电源电动势E＝20 V，内阻r＝1 Ω，当接入固定电阻R＝4 Ω时，电路中标有“3 V,6 W”的灯泡L和内阻RD＝0.5 Ω的小型直流电动机D都恰能正常工作．试求：
(1)电路中的电流大小；
(2)电动机的额定电压；
(3)电动机的输出功率．
如图所示，图甲为一个电灯两端电压与通过它的电流的变化关系曲线．由图可知，两者不成线性关系，这是由于焦耳热使灯丝的温度发生了变化的缘故，参考这条曲线回答下列问题(不计电流表内阻，线路提供电压不变)：
(1)若把三个这样的电灯串联后，接到电压恒定为12 V的电路上，求流过灯泡的电流和每个灯泡的电阻；
(2)如图乙所示，将两个这样的电灯并联后再与10 Ω的定值电阻R0串联，接在电压恒定为8 V的电路上，求通过电流表的电流值以及每个灯的实际功率．
粤公网安备 44130202000953号