如图所示,xOy坐标系中,第一象限有水平向右的匀强电场E1(大小未知)。第四象限半径分别为b与2b的两圆弧区域内有匀强磁场,磁感应强度为B,方向垂直xOy平面向里,第四象限还有方向竖直向下的匀强电场强度为E2(大小未知)。一质量为m,电量为q的微粒,从坐标(0,b)处以初速度v0垂直y轴射入第一象限。已知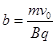 。
。
(1)如果带电微粒垂直x轴进入磁场,求E1的最大值与最小值;
(2)如果带电微粒既要垂直x轴进入磁场,又要垂直y轴离开磁场,且在磁场中做匀速圆周运动,求E2的值,E1的最大值。
如图所示,xOy坐标系中,第一象限有水平向右的匀强电场E1(大小未知)。第四象限半径分别为b与2b的两圆弧区域内有匀强磁场,磁感应强度为B,方向垂直xOy平面向里,第四象限还有方向竖直向下的匀强电场强度为E2(大小未知)。一质量为m,电量为q的微粒,从坐标(0,b)处以初速度v0垂直y轴射入第一象限。已知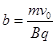 。
。
(1)如果带电微粒垂直x轴进入磁场,求E1的最大值与最小值;
(2)如果带电微粒既要垂直x轴进入磁场,又要垂直y轴离开磁场,且在磁场中做匀速圆周运动,求E2的值,E1的最大值。