如图所示,AB为半径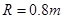 的1/4光滑圆弧轨道,下端B恰好与长度
的1/4光滑圆弧轨道,下端B恰好与长度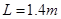 的小车右端平滑对接,小车质量
的小车右端平滑对接,小车质量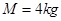 。现有一质量
。现有一质量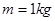 的小滑块,由轨道顶端无初速释放,滑到B端后冲上小车。已知地面光滑,滑块与小车上表面间的动摩擦因数
的小滑块,由轨道顶端无初速释放,滑到B端后冲上小车。已知地面光滑,滑块与小车上表面间的动摩擦因数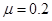 。(g=10m/s2)
。(g=10m/s2)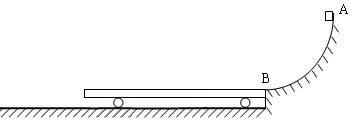
试求:(1)滑块到达B端时,它对轨道的压力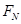 。
。
(2)经多长时间滑块从小车左端滑落。
如图所示,AB为半径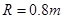 的1/4光滑圆弧轨道,下端B恰好与长度
的1/4光滑圆弧轨道,下端B恰好与长度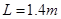 的小车右端平滑对接,小车质量
的小车右端平滑对接,小车质量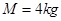 。现有一质量
。现有一质量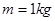 的小滑块,由轨道顶端无初速释放,滑到B端后冲上小车。已知地面光滑,滑块与小车上表面间的动摩擦因数
的小滑块,由轨道顶端无初速释放,滑到B端后冲上小车。已知地面光滑,滑块与小车上表面间的动摩擦因数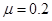 。(g=10m/s2)
。(g=10m/s2)
试求:(1)滑块到达B端时,它对轨道的压力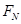 。
。
(2)经多长时间滑块从小车左端滑落。