如图是一组滑轮装置,绳子都处于竖直状态,不计绳子和滑轮质量及一切阻力,悬挂的两物体质量分别为 m1=m,m2=4m,m1下端通过劲度系数为k的轻质弹簧与地面相连(重力加速度为g,轻质弹簧始终处于弹性限度之内)求: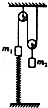
(1)系统处于静止时弹簧的形变量;
(2)用手托住m2且让m1静止在弹簧上,绳子绷直但无拉力,放手之后两物体的运动发生在同一竖直平面内,求m2运动的最大速度.
如图是一组滑轮装置,绳子都处于竖直状态,不计绳子和滑轮质量及一切阻力,悬挂的两物体质量分别为 m1=m,m2=4m,m1下端通过劲度系数为k的轻质弹簧与地面相连(重力加速度为g,轻质弹簧始终处于弹性限度之内)求:
(1)系统处于静止时弹簧的形变量;
(2)用手托住m2且让m1静止在弹簧上,绳子绷直但无拉力,放手之后两物体的运动发生在同一竖直平面内,求m2运动的最大速度.