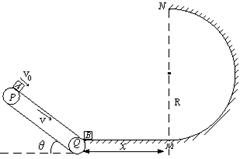
如图所示,一倾斜的传送带倾角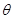 =37º,始终以
=37º,始终以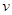 ="12" m/s的恒定速度顺时针转动,传送带两端点P、Q间的距离
="12" m/s的恒定速度顺时针转动,传送带两端点P、Q间的距离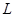 =2m,;紧靠Q点右侧有一水平面长
=2m,;紧靠Q点右侧有一水平面长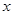 =2m,水平面右端与一光滑的半径
=2m,水平面右端与一光滑的半径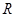 ="1.6" m的竖直半圆轨道相切于M点,MN为竖直的直径。现有一质量
="1.6" m的竖直半圆轨道相切于M点,MN为竖直的直径。现有一质量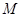 =2.5kg的物块A以
=2.5kg的物块A以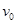 ="10" m/s的速度自P点沿传送带下滑,A与传送带间的动摩擦因数
="10" m/s的速度自P点沿传送带下滑,A与传送带间的动摩擦因数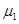 = 0.75,到Q点后滑上水平面(不计拐弯处的能量损失),并与静止在水平面左端的质量
= 0.75,到Q点后滑上水平面(不计拐弯处的能量损失),并与静止在水平面左端的质量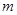 =0.5kg的B物块相碰,碰后A、B粘在一起,A、B与水平面的摩擦系数相同均为
=0.5kg的B物块相碰,碰后A、B粘在一起,A、B与水平面的摩擦系数相同均为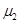 ,忽略物块的大小。已知sin37o=0.6,cos37o=0.8,求:
,忽略物块的大小。已知sin37o=0.6,cos37o=0.8,求:
(1)A滑上传送带时的加速度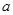 和到达Q点时的速度
和到达Q点时的速度
(2)若AB恰能通过半圆轨道的最高点N,求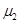
(3)要使AB能沿半圆轨道运动到N点,且从N点抛出后能落到传送带上,则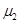 应满足什么条件?
应满足什么条件?
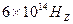 , 以
, 以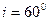 的入射角从甲介质射到乙介质的界面上,同时发生反射和折射,若反射线与折射线成90o角,波在甲介质中的波速为3.0×108m/s,求
的入射角从甲介质射到乙介质的界面上,同时发生反射和折射,若反射线与折射线成90o角,波在甲介质中的波速为3.0×108m/s,求


 的直线运动。现将该小球从电场中某点以初速度v0竖直向上抛出,求运动过程中(取sin37°=0.6,cos37°=0.8)
的直线运动。现将该小球从电场中某点以初速度v0竖直向上抛出,求运动过程中(取sin37°=0.6,cos37°=0.8)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号