如图所示，质量为mB=2kg的木块B静止在光滑水平面上。一质量为mA= 1kg的木块A以某一初速度v0=5m/s沿水平方向向右运动，与B碰撞后都向右运动。木块B 与挡板碰撞后立即反弹（设木块B与挡板碰撞过程无机械能损失）。后来木块B与A发生二次碰撞，碰后A、B同向运动，速度大小分别为1.2m/s 、0.9m/s。求：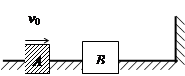
（ⅰ）第一次木块A、B碰撞过程中A对B的冲量大小和方向；
（ⅱ）木块A、B第一次碰撞过程中系统损失的机械能是多少？
（1）2011年3月16日上午10时福岛第一核电站第3号反应堆发生了爆炸引起社会恐慌，下）列关于核电站问题的说法正确的是（ ）
A、核电站发生的核反应方程为
B、可供研制核武器的钚239（
Pu），可以由铀239（
U）经过2次
衰变而产生
C、反应时产生的新核的平均结合能比发生反应的核的平均结合能小
D、核反应时产生大量的γ射线的本质是高速电子流
（2）如图所示，在光滑的水平桌面上有一长为L＝2 m的木板C，它的两端各有一块挡板，C的质量为mC＝5 kg，在C的中央并排放着两个可视为质点的滑块A与B，其质量分别为mA＝1 kg、mB＝4 kg，开始时A、B、C均处于静止状态，并且A、B间夹有少许炸药，炸药爆炸使得A以vA＝6 m/s的速度水平向左运动，不计一切摩擦，两滑块中任一块与挡板碰撞后就与挡板合成一体，爆炸与碰撞时间不计，求：
(1)当两滑块都与挡板碰撞后，板C的速度多大？
(2)从爆炸开始到两个滑块都与挡板碰撞为止，板C的位移多大？方向如何？
（1）如图所示，MN是位于竖直平面内的光屏，放在水平面上的半圆柱形玻璃砖的平面部分ab与屏平行．由光源S发出的一束白光从半圆沿半径射入玻璃砖，通过圆心O再射到屏上．在水平面内以O点为圆心沿逆时针方向缓缓转动玻璃砖，在光屏上出现了彩色光带．当玻璃砖转动角度大于某一值，屏上彩色光带中的某种颜色的色光首先消失．有关彩色的排列顺序和最先消失的色光是（ ）
A．左红右紫，红光 B．左红右紫，紫光 C．左紫右红，红光 D．左紫右红，紫光
（2）A、B两点相距6m，A处有一个做简谐振动的波源，当空间充有某种介质时，A点的振动经过0.5s传播到B点，此后A、B两点的振动方向始终相反；若空间充有另一种介质时，A点的振动经过0.6s传播到B点，此后A、B两点的振动始终相同，求这波源振动的最小频率。
在水平地面上方的足够大的真空室内存在着匀强电场和匀强磁场共存的区域，且电场与磁场的方向始终平行，在距离水平地面的某一高度处，有一个带电量为q、质量为m的带负电的质点，以垂直于电场方向的水平初速度v0进入该真空室内，取重力加速度为g。求：
（1）若要使带电质点进入真空室后做半径为R的匀速圆周运动，求磁感应强度B0的大小及所有可能的方向；
（2）当磁感应强度的大小变为B时，为保证带电质点进入真空室后做匀速直线运动，求此时电场强度E的大小和方向应满足的条件；
（3）若带电质点在满足第（2）问条件下运动到空中某一位置M点时立即撤去磁场，此后运动到空中另一位置N点时的速度大小为v，求M、N两点间的竖直高度H及经过N点时重力做功的功率。
如图所示，质量为M的铁箱内装有质量为m的货物．以某一初速度向上竖直抛出，上升的最大高度为H，下落过程的加速度大小为a，重力加速度为g，铁箱运动过程受到的空气阻力大小不变．求：
（1）铁箱下落过程经历的时间；
（2）铁箱和货物在落地前的运动过程中克服空气阻力做的功；
（3）上升过程货物受到铁箱的作用力．
如图，C1D1E1F1和C2D2E2F2是距离为L的相同光滑导轨，C1D1和E1F1为两段四分之一圆弧，半径分别为r1=8r和r2=r。在水平矩形D1E1E2D2内有竖直向上的匀强磁场，磁感应强度为B。导体棒P、Q的长度均为L，质量均为m，电阻均为R，其余电阻不计，Q停在图中位置，现将P从轨道最高点无初速释放，则
（1）求导体棒P进入磁场瞬间，回路中的电流的大小和方向（顺时针或逆时针）；
（2）若P、Q不会在轨道上发生碰撞，棒Q到达E1E2瞬间，恰能脱离轨道飞出，求导体棒P离开轨道瞬间的速度；
（3）若P、Q不会在轨道上发生碰撞，且两者到达E1E2瞬间，均
能脱离轨道飞出，求回路中产生热量的范围。
粤公网安备 44130202000953号