如图所示,两平行导轨间距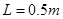 ,足够长光滑的倾斜部分和粗糙的水平部分圆滑连接,倾斜部分与水平面的夹角
,足够长光滑的倾斜部分和粗糙的水平部分圆滑连接,倾斜部分与水平面的夹角 ,垂直斜面方向向上的匀强磁场磁感应强度
,垂直斜面方向向上的匀强磁场磁感应强度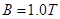 ,水平部分没有磁场,金属杆
,水平部分没有磁场,金属杆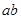 质量
质量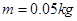 ,电阻
,电阻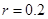 Ω,运动中与导轨始终接触良好,并且垂直于导轨。电阻
Ω,运动中与导轨始终接触良好,并且垂直于导轨。电阻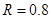 Ω,导轨电阻不计。当金属棒从斜面上距底面高
Ω,导轨电阻不计。当金属棒从斜面上距底面高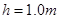 以上的任何地方由静止释放后,在水平面上滑行的最大距离
以上的任何地方由静止释放后,在水平面上滑行的最大距离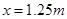 ,取
,取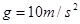 ,求:
,求: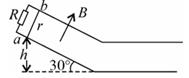
(1)金属棒在斜面上的最大运动速度;
(2)金属棒与水平导轨间的动摩擦因素;
(3)若金属棒从高度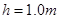 处由静止释放,电阻
处由静止释放,电阻 产生的热量.
产生的热量.
如图所示,两平行导轨间距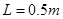 ,足够长光滑的倾斜部分和粗糙的水平部分圆滑连接,倾斜部分与水平面的夹角
,足够长光滑的倾斜部分和粗糙的水平部分圆滑连接,倾斜部分与水平面的夹角 ,垂直斜面方向向上的匀强磁场磁感应强度
,垂直斜面方向向上的匀强磁场磁感应强度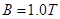 ,水平部分没有磁场,金属杆
,水平部分没有磁场,金属杆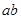 质量
质量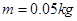 ,电阻
,电阻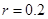 Ω,运动中与导轨始终接触良好,并且垂直于导轨。电阻
Ω,运动中与导轨始终接触良好,并且垂直于导轨。电阻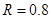 Ω,导轨电阻不计。当金属棒从斜面上距底面高
Ω,导轨电阻不计。当金属棒从斜面上距底面高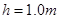 以上的任何地方由静止释放后,在水平面上滑行的最大距离
以上的任何地方由静止释放后,在水平面上滑行的最大距离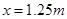 ,取
,取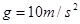 ,求:
,求:
(1)金属棒在斜面上的最大运动速度;
(2)金属棒与水平导轨间的动摩擦因素;
(3)若金属棒从高度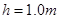 处由静止释放,电阻
处由静止释放,电阻 产生的热量.
产生的热量.