如图所示,在0≤ x≤ a、0≤ y≤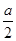 范围内有垂直于xOy平面向外的匀强磁场,磁感应强度大小为B.坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0~90°范围内.已知粒子在磁场中做圆周运动的半径介于
范围内有垂直于xOy平面向外的匀强磁场,磁感应强度大小为B.坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0~90°范围内.已知粒子在磁场中做圆周运动的半径介于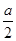 到a之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一.求最后离开磁场的粒子从粒子源射出时的:
到a之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一.求最后离开磁场的粒子从粒子源射出时的: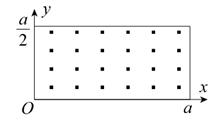
(1)速度大小;
(2)速度方向与y轴正方向夹角的正弦.
如图所示,在0≤ x≤ a、0≤ y≤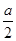 范围内有垂直于xOy平面向外的匀强磁场,磁感应强度大小为B.坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0~90°范围内.已知粒子在磁场中做圆周运动的半径介于
范围内有垂直于xOy平面向外的匀强磁场,磁感应强度大小为B.坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0~90°范围内.已知粒子在磁场中做圆周运动的半径介于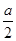 到a之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一.求最后离开磁场的粒子从粒子源射出时的:
到a之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一.求最后离开磁场的粒子从粒子源射出时的:
(1)速度大小;
(2)速度方向与y轴正方向夹角的正弦.