如图，一不可伸长的轻绳上端悬挂于O点，下端系一质量m＝1.0kg的小球。现将小球拉到A点(保持绳绷直)由静止释放，当它经过B点时绳恰好被拉断，小球平抛后落在水平地面上的C点。地面上的D点与OB在同一竖直线上，已知绳长L＝1.0m，B点离地高度H＝1.0m，A、B两点的高度差h＝0.5m，重力加速度g取10m/s2，不计空气阻力影响，求：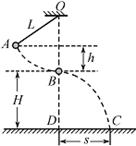
⑴地面上DC两点间的距离s；⑵轻绳所受的最大拉力大小。
如图所示的匀强电场中，有A.B.c三点，ab＝5 cm，bc＝12 cm，其中ab沿电场线方向，bc和电场线方向成60°角，一个电荷量为q＝4×10－8 C的正电荷从a点移到b点时静电力做功为W1＝1.2×10－7 J，求：
(1)匀强电场的场强E；
(2)电荷从b移到c，静电力做功W2；
(3)A.c两点间的电势差Uac.
竖直放置的两块足够长的平行金属板间有匀强电场．其电场强度为E，在该匀强电场中，用丝线悬挂质量为m的带电小球，丝线跟竖直方向成θ角时小球恰好平衡，如图所示．
(1)小球带电荷量是多少？
(2)若剪断丝线，小球碰到金属板需多长时间？
如图所示，质量MA=2m的直杆A悬于离地面很高处，杆A上套有质量MB=m的小环B。将小环B由静止释放，环做加速度a=3/4g的匀加速运动。经过时间
后，将杆A上方的细线剪断，杆A开始下落。杆A足够长，环B始终未脱离杆A，不计空气阻力，已知重力加速度为g，求：
(1)杆A刚下落时的加速度a'；
(2)在小环B下落的整个过程中，环B对杆A所做的功W;
(3)在小环B下落的整个过程中，系统产生的热量Q。
（由于地球自转的影响，地球表面的重力加速度会随纬度的变化而有所不同：若地球表面两极处的重力加速度大小为g0，在赤道处的重力加速度大小为g，地球自转的周期为T，引力常量为G，地球可视为质量均匀分布的球体。求： (1)地球半径R；(2)地球的平均密度；
(3)若地球自转速度加快，当赤道上的物体恰好能“飘”起来时，求地球自转周期T'。
粤公网安备 44130202000953号