如图所示,光滑水平面上静止着一辆质量为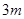 的平板车A。车上有两个小滑块B和C(都可视为质点),B的质量为
的平板车A。车上有两个小滑块B和C(都可视为质点),B的质量为 ,与车板之间的动摩擦因数为
,与车板之间的动摩擦因数为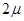 。C的质量为
。C的质量为 ,与车板之间的动摩擦因数为
,与车板之间的动摩擦因数为 。t=0时刻B、C分别从车板的左、右两端同时以初速度
。t=0时刻B、C分别从车板的左、右两端同时以初速度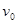 和
和 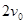 相向滑上小车。在以后的运动过程中B与C恰好没有相碰。已知重力加速度为g, 设最大静摩擦力与滑动摩擦力大小相等。求:
相向滑上小车。在以后的运动过程中B与C恰好没有相碰。已知重力加速度为g, 设最大静摩擦力与滑动摩擦力大小相等。求:
(1)平板车的最大速度 和达到最大速度经历的时间;
和达到最大速度经历的时间;
(2)平板车平板总长度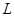 ;
;
如图所示,光滑水平面上静止着一辆质量为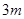 的平板车A。车上有两个小滑块B和C(都可视为质点),B的质量为
的平板车A。车上有两个小滑块B和C(都可视为质点),B的质量为 ,与车板之间的动摩擦因数为
,与车板之间的动摩擦因数为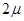 。C的质量为
。C的质量为 ,与车板之间的动摩擦因数为
,与车板之间的动摩擦因数为 。t=0时刻B、C分别从车板的左、右两端同时以初速度
。t=0时刻B、C分别从车板的左、右两端同时以初速度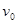 和
和 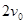 相向滑上小车。在以后的运动过程中B与C恰好没有相碰。已知重力加速度为g, 设最大静摩擦力与滑动摩擦力大小相等。求:
相向滑上小车。在以后的运动过程中B与C恰好没有相碰。已知重力加速度为g, 设最大静摩擦力与滑动摩擦力大小相等。求:
(1)平板车的最大速度 和达到最大速度经历的时间;
和达到最大速度经历的时间;
(2)平板车平板总长度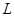 ;
;