(14分)如图所示，木板与水平地面间的夹角θ可以随意改变，当θ=30°时，可视为质点的一小木块恰好能沿着木板匀速下滑。若让该小木块从木板的底端以大小恒定的初速率v0=10m/s的速度沿木板向上运动，随着θ的改变，小物块沿木板滑行的距离x将发生变化，重力加速度g=10m/s2。(结果可用根号表示)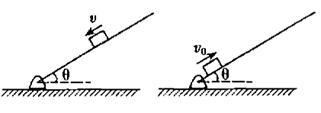
（1）求小物块与木板间的动摩擦因数；
（2）当θ角满足什么条件时，小物块沿木板滑行的距离最小，并求出此最小值。
如图所示，电源电动势E=8V，内电阻为r=0.5Ω，“3V,3W”的灯泡L与电动机M串联接在电源上，灯泡刚好正常发光，电动机刚好正常工作，电动机的线圈电阻R0=1.5Ω。
求：（1）通过电动机的电流
（2）电源的输出功率
（3）电动机的输出功率
如图所示，一质量为m的带电小球，用绝缘细线悬挂在水平向右的匀强电场中，静止时悬线与竖直方向成
角．已知电场强度为E，重力加速度为g
(1)小球带正电荷还是带负电荷?
(2)求小球所带电荷量的大小．
(3)将细线突然剪断的瞬间，求小球的加速度大小
(13分)如图所示，AB是一段位于竖直平面内的光滑轨道，高度为h，末端B处的切线方向水平．一个质量为m的小物体P从轨道顶端A处由静止释放，滑到B端后飞出，落到地面上的C点，轨迹如图中虚线BC所示．已知它落地时相对于B点的水平位移OC＝l．现在轨道下方紧贴B点安装一水平传送带，传送带的右端与B的距离为l／2．当传送带静止时，让P再次从A点由静止释放，它离开轨道并在传送带上滑行后从右端水平飞出，仍然落在地面的C点．当驱动轮转动从而带动传送带以速度
匀速向右运动时（其他条件不变），P的落地点为D．（不计空气阻力）
（1）求P滑至B点时的速度大小；
（2）求P与传送带之间的动摩擦因数；
（3）求出O、D间的距离．
(11分)如图所示，一长绝缘木板靠在光滑竖直墙面上，质量为
。木板右下方有一质量为
、电荷量为
的小滑块，滑块与木板间的动摩擦因数为
，木板与滑块处在场强大小为
的匀强电场中，电场方向水平向左，若电动机通过一根绝缘细绳拉动滑块，使之匀加速向上移动，当滑块与木板分离时，滑块的速度大小为
，此过程中电动机对滑块的做功为
（重力加速度为
）
（1）求滑块向上移动的加速度大小；
（2）写出从滑块开始运动到与木板分离的过程中木板增加的机械能随时间变化的函数关系式。
.1 kg,细线总长为20 cm,现将绝缘细线绕过固定于O点的光滑定滑轮,将两球悬挂起来,两球平衡时,OA的线长等于OB的线长,A球依于光滑绝缘竖直墙上,B球悬线OB偏离竖直方向60○,求B球的质量和墙所受A球的压力(g取10 N/kg). 
粤公网安备 44130202000953号