如图所示，有一半径为r的圆形有界匀强磁场区域，磁感应强度为B，方向垂直纸面向里，其周围对称放置带有中心孔a、b、c的三个相同的平行板电容器，三个电容器两板间距离均为d，接有相同的电压U，在D处有一静止的电子，质量为m，电荷量为e，释放后从a孔射入匀强磁场中，并先后穿过b、c孔再从a孔穿出回到D处，求：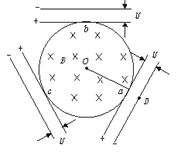
（1）电子在匀强磁场中运动的轨道半径R；
（2）匀强磁场的磁感应强度B；
（3）电子从D出发到第一次回到D处所用的时间t。
如图所示，水平轨道AB与竖直轨道CD用一光滑的半径R＝0．5m的
圆弧BC平滑连接，现有一物块从竖直轨道上的Q点由静止开始释放，已知QC间的长度R＝0．5m，物块的质量m＝0．2kg，物块与AB和CD轨道间的动摩擦因数均为μ＝0．5，重力加速度g取10m／s2，求；
（1）物块下滑到水平面后，距离B点的最远距离s为多少?
（2）若整个空间存在一水平向右的匀强电场，电场强度E＝1．0×106V／m，并使物块带电，带电量为q＝＋2．0×10－6C，所有接触面均绝缘，现使带电物块从水平面上的P点由静止开始释放（P点未在图中标出），要想使物块刚好能通过Q点，PB间的长度L为多少?
（3）在符合第二问的基础上，物块到达圆弧上C点时，对轨道的压力大小?
在平面直角坐标系xOy中，第Ⅰ象限存在沿y轴负方向的匀强电场，第Ⅳ象限存在垂直于坐标平面向外的匀强磁场，磁感应强度为B。一质量为m．电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场，经x轴上的N点与x轴正方向成θ＝60°角射入磁场，最后从y轴负半轴上的P点垂直于y轴射出磁场，如图所示。不计粒子重力，求：
（1）粒子过N点时速度；
（2）粒子在磁场中运动的轨道半径r；
（3）粒子从M点运动到P点的总时间t。
水平放置的平行金属框架L=0.2m,质量为0.1kg的金属棒ab放在框架上，并且与框架的两个边垂直。整个装置放于方向竖直向下、B=0.5T的匀强磁场中，如图所示。金属棒ab在F=2N的水平向右的恒力作用下由静止开始运动。电路中除R=0.05
外，其他电阻、摩擦阻力均不考虑。求：
① ab速度是5m/s时，棒的加速度是多大？
② 当ab棒达到最大速度后，撤去外力F，此后感应电流还能产生多少热量？
如图所示，一电子（电荷量数值为e，质量为m）以速度
垂直射入宽度为d的匀强磁场中，磁场上、下方向范围无限大，穿出磁场时的速度方向与电子原来入射时的速度方向间的夹角是30°，则匀强磁场的磁感应强度为多大？穿过磁场的时间是多长？
粤公网安备 44130202000953号