如图所示，在同一均匀介质中有S1和S2两个波源，这两个波源的频率、振动方向均相同，且振动的步调完全一致，S1与S2之间相距为4 m，若S1、S2振动频率均为5 Hz，两列波的波速均为10 m/s，B点为S1和S2连线的中点，今以B点为圆心，以R＝BS1为半径画圆．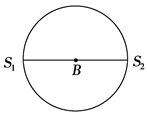
(1)该波的波长为多少？
(2)在S1、S2连线上振动加强的点有几个，它们距S1的距离为多少？
(3)在该圆周上(S1和S2两波源除外)共有几个振动加强的点？
如图所示，轨道ABC被竖直地固定在水平桌面上，A距离水平地面高H =" 0.75" m，C距离水平地面高h =" 0.45" m。一质量m = 0.10kg的小物块自A点由静止开始下滑，从C点以水平速度飞出后落在水平地面上的D点
。现测得C、D两点的水平距离为l =" 0.60" m。不计空气阻力，取g =" 10" m/s2。求：
（1）小物块从C点运动到D点经历的时间；
（2）小物块从C点飞出时速度的大小；
（3）小物块从A点运动到C点的过程中克服摩擦力做的功。
月球自转一周的时间与月球绕地球运行一周的时间相等，都为T0。“
嫦娥1号”探月卫星于2007年11月7日成功进入绕月运行的“极月圆轨道”，这一圆形轨道通过月球两极上空，距月面的高度为h。若月球质量为M，月球半径为R，万有引力恒量为G。求：
（1）“嫦娥1号”绕月运行的周期。
（2）在月球自转一周的过程中，“嫦娥1号”将绕月运行多少圈？
游乐场的过山车可以底朝上在圆轨道上运行，游客却不会掉下来，如图甲所示。我们把这种情况抽象为如图乙所示的模型：半径为R的圆弧轨道竖直放置，下端与弧形轨道相接，使质量为m的小球从弧形轨道上端无初速度滚下，小球进入圆轨道下端后沿圆轨道运动。实验表明，只要h大于一定值，小球就可以顺利通过圆轨道的最高点。（不考虑空气及摩擦阻力）
（1）若小球恰能通过最高点，则小球在最高点的速度为多大? 此时对应的h多高？
（2）若h′=4R，则小球在通过圆轨道的最高点时对轨道的压力是多少？
将小球从离地面5m高处、向离小球4m远的竖直墙以8m/s的初速度水平抛出，不计空气阻力。求：（g=10m/s2）
（1）小球碰墙点离地面的高度；
（2）要使小球不碰墙，小球的最大初速度。
粤公网安备 44130202000953号