如图所示，质量为m、半径为R的光滑半圆形轨道A静置于光滑水平面上，质量为
的物块B（可视为质点）从轨道右端从静止开始释放，求物块B滑至轨道最低处时：
（1）A、B的速度大小vA、vB； （2）B对轨道压力大小．
如图所示装置由AB、BC、CD三段轨道组成，轨道交接处均由很小的圆弧平滑连接，其中轨道AB、CD段是光滑的，水平轨道BC的长度s=5m，轨道CD足够长且倾角θ=37°，A、D两点离轨道BC的高度分别为
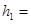4.30m、
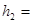1.35m。现让质量为m的小滑块自A点由静止释放。已知小滑块与轨道BC间的动摩擦因数μ=0.5，重力加速度g取10m/s2，sin37°=0.6、cos37°=0.8。求：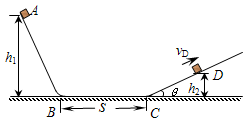
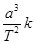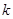（1）小滑块第一次到达D点时的速度大小；
（2）小滑块第一次与第二次通过C点的时间间隔；
（3）小滑块最终停止的位置距B点的距离。
（1）开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比，即
, 
是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理，请你推导出太阳系中该常量的表达式。已知引力常量为G，太阳的质量为M太。
（2）开普勒定律不仅适用于太阳系，它对一切具有中心天体的引力系统（如地月系统）都成立。经测
定月地距离为3．84×108m，月球绕地球运动的周期为2．36×106s，试计算地球的质量M地。（G=6．67
×10-11N·m2/kg2，结果保留一位有效数字）
(14分) 如图所示，足够长的两根相距为0.5m的平行光滑导轨竖直放置，导轨电阻不计，磁感应强度B为0.8T的匀强磁场的方向垂直于导轨平面。两根质量均为0.04kg、电阻均为0.5Ω的可动金属棒
和
都与导轨始终接触良好，导轨下端连接阻值为1Ω的电阻R，金属棒用一根细绳拉住，细绳允许承受的最大拉力为0.64N。现让棒从静止开始落下，直至细绳刚被拉断时，此过程中电阻R上产生的热量为0.2J，（g=10m/s2）求：
（1）此过程中棒和棒产生的热量
和
；
（2）细绳被拉断瞬时，棒的速度
。
（3）细绳刚要被拉断时，棒下落的高度
。
如图所示，水平放置的两块长直平行金属板a、b相距d=0.10m，a、b间的电场强度为E=5.0×105N/C，b板下方整个空间存在着磁感应强度大小为B=6.0T、方向垂直纸面向里的匀强磁场.今有一质量为m=4.8×10-25kg、电荷量为q=1.6×10-18C的带正电的粒子(不计重力)，从贴近a板的左端以v0 =1.0×106m/s的初速度水平射入匀强电场，刚好从狭缝P处穿过b板而垂直进入匀强磁场，最后粒子回到b板的Q处（图中未画出）．求P、Q之间的距离L．
粤公网安备 44130202000953号